如图,已知四棱锥P-ABCD的底面为菱形,且∠ABC =60°,AB=PC=2,AP=BP=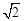 .
.
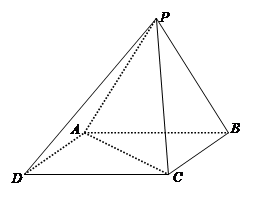
(Ⅰ)求证:平面PAB⊥平面ABCD ;
(Ⅱ)求二面角A-PC-D的平面角的余弦值.
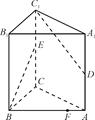
如图所示,在正方体ABCDA1B1C1D1中,E、F、G、H分别是BC、CC1、C1D1、A1A的中点.求证:
(1)BF∥HD1;
(2)EG∥平面BB1D1D.
如图所示,在三棱柱ABCA1B1C1中,M、N分别是BC和A1B1的中点.求证:MN∥平面AA1C1.
如图,在三棱柱ABC-A1B1C1中,D是BC的中点.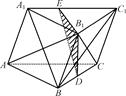
(1)若E为A1C1的中点,求证:DE∥平面ABB1A1;
(2)若E为A1C1上一点,且A1B∥平面B1DE,求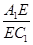 的值..
的值..
正三棱柱ABCA1B1C1中,已知AB=A1A,D为C1C的中点,O为A1B与AB1的交点.
(1)求证:AB1⊥平面A1BD;
(2)若点E为AO的中点,求证:EC∥平面A1BD.
如图所示,在直三棱柱ABCA1B1C1中,D、E分别为AA1、CC1的中点,AC⊥BE,点F在线段AB上,且AB=4AF.若M为线段BE上一点,试确定M在线段BE上的位置,使得C1D∥平面B1FM.