如图,正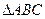 的中线
的中线 与中位线
与中位线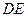 相交
相交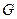 ,
,
已知 是
是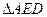 绕
绕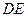 旋转过程中的一个
旋转过程中的一个
图形(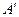 不与
不与 重合).现给出下列四个命题:
重合).现给出下列四个命题:
①动点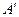 在平面
在平面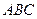 上的射影在线段
上的射影在线段 上;
上;
②平面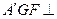 平面
平面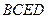 ;
;
③三棱锥 的体积有最大值;
的体积有最大值;
④异面直线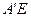 与
与 不可能垂直.其中正确的命题的序号是_________.
不可能垂直.其中正确的命题的序号是_________.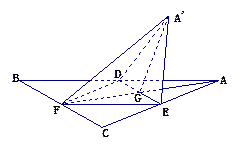
给定集合 ,映射
,映射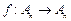 满足:
满足:
①当 时,
时, ;
;
②任取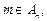 若
若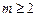 ,则有
,则有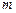
 .
.
.则称映射 :
: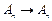 是一个“优映射”.例如:用表1表示的映射
是一个“优映射”.例如:用表1表示的映射 :
: 是一个“优映射”.
是一个“优映射”.
表1表2
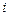 |
1 |
2 |
3 |
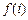 |
2 |
3 |
1 |
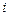 |
1 |
2 |
3 |
4 |
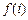 |
3 |
(1)已知表2表示的映射 :
: 是一个优映射,请把表2补充完整(只需填出一个满足条件的映射);
是一个优映射,请把表2补充完整(只需填出一个满足条件的映射);
(2)若映射 :
: 是“优映射”,且方程
是“优映射”,且方程 的解恰有6个,则这样的“优映射”的个数是_____.
的解恰有6个,则这样的“优映射”的个数是_____.
在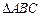 中,角
中,角 ,
,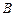 ,
, 所对应的边分别为
所对应的边分别为 ,
, ,
, ,若
,若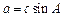 ,则
,则 的最大值为.
的最大值为.
已知数列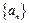 满足
满足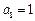 ,
, (
(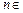 N
N ),则
),则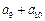 的值为.
的值为.
已知向量a=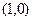 ,b=
,b=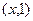 ,若
,若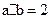 ,则
,则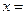 ;
;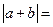 .
.
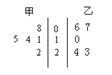
某校高中年级开设了丰富多彩的校本课程,甲、乙两班各随机抽取了5名学生的学分,用茎叶图表示(如右图).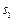 ,
,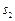
 分别表示甲、乙两班各自5名学生学分的标准差,则
分别表示甲、乙两班各自5名学生学分的标准差,则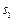
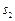 .(填“
.(填“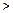 ”、“
”、“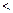 ”或“=”)
”或“=”)