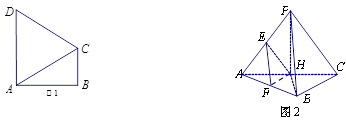如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB= (
( 2),BC=2,且AE=AH=CF=CG,设AE=
2),BC=2,且AE=AH=CF=CG,设AE=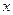 ,绿地面积为
,绿地面积为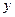 .
.
(1)写出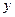 关于
关于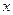 的函数关系式,指出这个函数的定义域.
的函数关系式,指出这个函数的定义域.
(2)当AE为何值时,绿地面积最大?
已知等差数列{an}的前n项和为 Sn
(I)若a1=1,S10= 100,求{an}的通项公式;
(II)若Sn=n2-6n,解关于n的不等式Sn+an>2n
设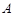 是由
是由 个实数组成的
个实数组成的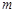 行
行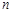 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(Ⅰ) 数表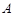 如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
表1
| 1 |
2 |
3 |
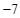 |
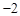 |
1 |
0 |
1 |
(Ⅱ) 数表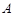 如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数
如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数 的所有可能值;
的所有可能值;
表2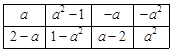
(Ⅲ)对由 个实数组成的
个实数组成的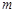 行
行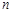 列的任意一个数表
列的任意一个数表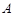 ,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由.
,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由.
已知椭圆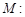
 的四个顶点恰好是一边长为2,一内角为
的四个顶点恰好是一边长为2,一内角为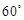 的菱形的四个顶点.
的菱形的四个顶点.
(I)求椭圆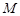 的方程;
的方程;
(II)直线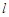 与椭圆
与椭圆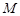 交于
交于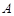 ,
,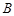 两点,且线段
两点,且线段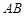 的垂直平分线经过点
的垂直平分线经过点 ,求
,求 (
(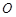 为原点)面积的最大值.
为原点)面积的最大值.
已知函数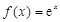 ,点
,点 为一定点,直线
为一定点,直线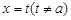 分别与函数
分别与函数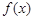 的图象和
的图象和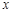 轴交于点
轴交于点 ,
,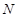 ,记
,记 的面积为
的面积为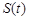 .
.
(I)当 时,求函数
时,求函数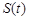 的单调区间;
的单调区间;
(II)当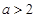 时, 若
时, 若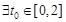 ,使得
,使得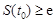 , 求实数
, 求实数 的取值范围.
的取值范围.
如图1,在直角梯形 中,
中,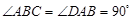 ,
, ,
,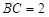 ,
,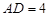 . 把
. 把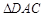 沿对角线
沿对角线 折起到
折起到 的位置,如图2所示,使得点
的位置,如图2所示,使得点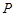 在平面
在平面 上的正投影
上的正投影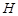 恰好落在线段
恰好落在线段 上,连接
上,连接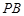 ,点
,点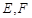 分别为线段
分别为线段 的中点.
的中点.
(I)求证:平面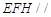 平面
平面 ;
;
(II)求直线 与平面
与平面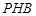 所成角的正弦值;
所成角的正弦值;
(III)在棱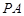 上是否存在一点
上是否存在一点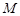 ,使得
,使得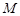 到点
到点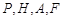 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.