如图所示,三边长均为L=0.6m的光滑U形导轨Ⅰ固定放置,与水平面成60°角;
另一足够长的光滑U形导轨Ⅱ固定放置在比导轨Ⅰ高的水平面内,导轨Ⅱ内始终存在着水平向右作匀加速运动的匀强磁场,磁感应强度B'= 1.0T,方向竖直向上,质量为m=0.1kg,阻值为R=2.0Ω的导体棒ab垂直导轨放置在导轨Ⅰ的开口处(有两柱挡着ab),现突然在导轨Ⅰ内加一垂直于导轨Ⅰ平面向上的、以B=B0-10t变化的磁场,经0.1s后,ab棒离开导轨Ⅰ斜向上飞出(在该0.1s内,导体棒ab所受的安培力大于其重力沿导轨Ⅰ所在平面的分力),恰好能到达最高点时落在导轨Ⅱ的开口a'b'处,此后,ab棒及匀强磁场B'运动的v-t图象分别为图乙中的平行线①②.若ab棒始终与导轨接触良好,导轨的电阻和空气阻力均不计。g取10m/s2,求:
(1)ab棒飞起的高度h;
(2)磁场B的初始值B0;
(3)磁场B'向右运动的加速度a。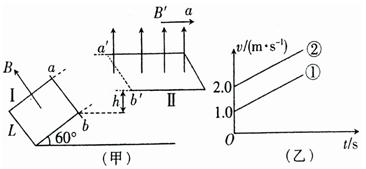
一辆质量为2.0×103kg的汽车以额定功率为6.0×104W在水平公路上行驶,汽车受到的阻力为一定值,在某时刻汽车的速度为20m/s,加速度为0.50m/s2,(g取10m/s2)求:
(1) 汽车受到的阻力是多大?
(2)汽车所能达到的最大速度是多大?
(3)当汽车的速度为10m/s时的加速度是多大?
一个质量为2kg的物体静止在光滑的水平面上,在6N的水平恒力F的作用下开始运动,求:
(1)2s内力F对物体做多少功
(2)力F在2s内的平均功率
(3)力F在2s末的功率
在“北斗”卫星导航系统中,同步卫星起到非常重要的作用,这些卫星运动在离地心的距离为r的圆形轨道上。已知某颗同步卫星的质量m,引力常量G,地球自转周期为T,请根据以上信息,求出下列物理量(用题中给出的物理量表示)。求:(1)同步卫星运动的角速度大小;
(2)地球对该卫星的吸引力大小;
(3)地球的质量大小。
如图,一质量为m=10kg的物体,由1/4圆弧轨道上端从静止开始下滑,到达底端时的速度v=3m/s,然后沿水平面向右滑动1m距离后停止。已知轨道半径R=0.5m,则: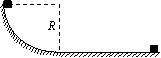
(1)物体沿圆弧轨道下滑过程中克服摩擦力做多少功;
(2)物体滑至圆弧底端时对轨道的压力是多大;
(3)物体与水平面间的动摩擦因数μ是多少。
质量m=1吨的汽车通过圆形拱形桥时的速率恒定,拱形桥的半径R=5m。试求: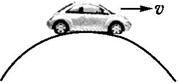
(1)汽车在最高点对拱形桥的压力为车重的一半时汽车的速度;
(2)汽车在最高点对拱形桥的压力为零时汽车的速度。