如下图所示,一根原长l="0.1" m的轻弹簧,一端挂质量m="0.5" kg的小球,以另一端为圆心在光滑水平面上做匀速圆周运动,角速度ω="10" rad/s.已知弹簧的劲度k="100" N/m,求小球受到的向心力大小.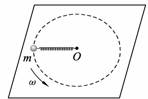
一列简谐横波,在t=0.4 s时刻的波形图象如图乙所示,波上A质点的振动图象如图甲所示,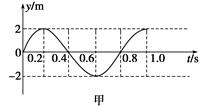

(1)判断该波的传播方向;
(2)求该波的传播速度.
如图所示,让摆球从图中的A位置由静止开始下摆,正好摆到最低点B位置时线被拉断.设摆线长ι=1.6 m,悬点到地面的竖直高度为H=6.6 m,不计空气阻力,求: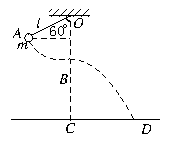
(1)摆球落地时的速度的大小.
(2)落地点D到C点的距离(g=10 m/s2).
如图所示,倾角为θ的光滑斜面上放有两个质量均为m的小球A、B,两小球用一根长L的轻杆相连,下面的B球离斜面底端的高度为h,两球从静止开始下滑并从斜面进入光滑平面(不计与地面碰撞时的机械能损失).求:
(1)两球在光滑平面上运动时的速度;
(2)在这过程中杆对A球所做的功;
(3)杆对A做功所处的时间段(仅文字说明,不计算).
如图所示,轻弹簧k一端与墙相连,处于自然状态,质量为4 kg的木块沿光滑的水平面以5m/s的速度运动并开始挤压弹簧.求弹簧的最大弹性势能及木块被弹回速度增大到3m/s时弹簧的弹性势能.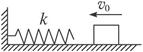
某人站在离地面h="10" m高处的平台上以速度v0=5m/s水平抛出一个质量m=1kg的小球,不计空气阻力,g取10 m/s2.问:
(1)人对小球做了多少功?
(2)小球落地时的速度为多大?