一机器可以按各种不同速度运转，其生产的产品有一些会有缺点，每小时生产有缺点的产品数随机器运转速度的不同而变化。下表为其试验数据：
| 速度（x转/秒） |
每小时生产有缺点的产品数（y个） |
||
| 8 |
6 |
||
| 9 |
8 |
||
| 10 |
10 |
||
| 13 |
12 |
（1）、画出散点图；
（2）、求机器运转速度与每小时生产有缺点的产品数之间的回归方程；（系数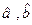
用分数表示）
（3）、若实际生产所允许的每小时生产有缺点的产品数不超过10件，那么机器的速度每秒不超过多少转？
在平面内，如果用一条直线去截正方形的一个角，那么截下的一个直角三角形按图所标边长，由勾股定理有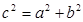
。设想正方形换成正方体，把截线换成如图所示的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥
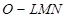，如果用
，
，
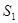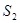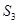表示三个侧面面积，
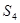表示截面面积，那么你类比得到的结论是。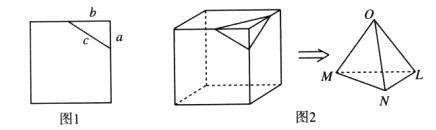
在数列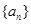
中，对于任意
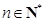，等式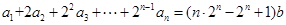
成立，其中常数
.
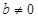（Ⅰ）求
的值；
（Ⅱ）求证：数列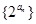
为等比数列；
（Ⅲ）如果关于n的不等式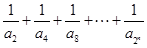
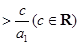的解集为
，求b和c的取值范围.
设函数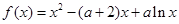
，其中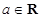
.
（Ⅰ）若函数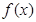
的图象在点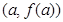
处的切线与直线
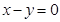平行，求实数
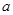的值；
（Ⅱ）求函数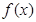的极值.
如图，要建一间体积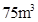为
，墙高为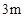
的长方体形的简易仓库. 已知仓库屋顶每平方米的造价为500元，墙壁每平方米的造价为400元，地面造价忽略不计. 问怎样设计仓库地面的长与宽，能使总造价最低？最低造价是多少？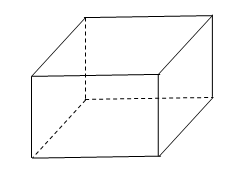
已知函数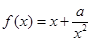
，其中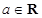
.
（Ⅰ）若函数
为奇函数，求实数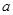
的值；
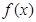（Ⅱ）若函数在区间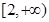
上单调递增，求实数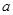的取值范围.
