（本小题满分12分）
甲、乙、丙三人进行某项比赛，每局有两人参加，没有平局，在一局比赛中甲胜乙的概率为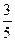
，甲胜丙的概
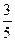，乙胜丙的概率为，比赛的规则是先由甲和乙进行第一局的比赛，然后每局的获胜者与
未参加此局比赛的人进行下一局的比赛，在比赛中，有人获胜两局就算取得比赛的胜利，比赛结束
网]
试判断下列函数的奇偶性：
⑴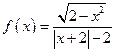
某出版社的7名工人中，有3人只会排版，2人只会印刷，还有2人既会排版又会印刷，现从7人中安排2人排版，2人印刷，有几种不同的安排方法．
某校学生会由高一年级5人，高二年级6人，高三年级4人组成．
（1）选其中1人为学生会主席，有多少种不同的选法？
（2）若每年级选1人为校学生会常委，有多少种不同的选法？
（3）若要选出不同年级的两人参加市里组织的活动，有多少种不同的选法？
一个口袋内装有5个小球，另一个口袋内装有4个小球，所有这些小球的颜色互不相同．
（1）从两个口袋内任取一个小球，有多少种不同的取法？
（2）从两个口袋内各取一个小球，有多少种不同的取法？
某学生计算一离散型随机变量X的分布列如表：
 |
 |
0 |
1 |
2 |
 |
 |
 |
|
|
试说明该学生的计算是否正确；如果不正确，请说明理由．