某工厂建一个长方形无盖蓄水池,其容积为4800m3,深度为3m。如果池底每1 m2的造价为150元,池壁每1 m2的造价为120元,怎么设计水池能使造价最低?最低造价多少元?
已知函数
(1)在锐角 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边;若
的对边;若 ,sin(A
,sin(A C)=
C)= sinC,求
sinC,求 的面积.
的面积.
(2)若 ,求
,求 的值;
的值;
设数列 的前
的前 项和为
项和为 ,且满足
,且满足 (
( =1,2,3,…).
=1,2,3,…).
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,且
,且 ,求数列
,求数列 的通项公式;
的通项公式;
(本小题满分12分)某木材加工厂为了提高生产高效率和产品质量,决定添置一台125000元的新木材加工机器。若机器第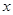 天的维护费为
天的维护费为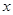 元,则该机器使用多少天能使平均每天的支出最少?
元,则该机器使用多少天能使平均每天的支出最少?
(本小题满分12分)已知等差数列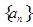 的第2项为8 ,前10项和为185,从数列
的第2项为8 ,前10项和为185,从数列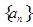 中依次取出第2项,4 项,8项,……,第
中依次取出第2项,4 项,8项,……,第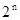 项 ,按原来顺序排成一个新数列
项 ,按原来顺序排成一个新数列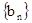 ,
,
(1)分别求出数列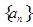 、
、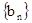 的通项公式,
的通项公式,
(2)求 数列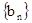 的前n项和
的前n项和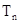 。
。
(本小题满分12分)已知不等式ax2-3x+2>0的解集为{x|x<1或x>b},
(1)求a,b;
(2)解不等式ax2-(ac+b)x+bc<0.