（本小题10分）
已知甲、乙两地相距150km，某人开汽车以6
0km/h的速度从
甲地到达乙地，在乙地停留1小时后再以50km/h的速度返回甲地，把汽车离开甲地的距离s表示为时间t（从甲地出发时开始）的函数，求此函数表达式．
已知
求
的值。
（本小题满分12分）已知函数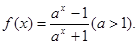
（1）判断函数的奇偶性；
（2）求该函数的值域；
（3）证明
是R上的增函数。
（本小题满分10分）设集合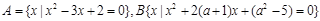 
（1）若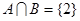
，求实数a的值；
（2）若
，求实数a的取值范围。
（本小题满分14分）已知函数
（Ⅰ）当
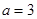时，求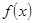
的单调增区间；（Ⅱ）若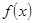在
上是增函数，求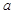
得取值范围；（Ⅲ）
在（Ⅱ）的结论下，设
，求函数
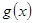的最小值.
（本小题满分13分）已知椭圆C的中心在坐标原点，离心率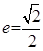
，且其中一个焦点与抛物线
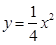的焦点重合．(Ⅰ)求椭圆C的方程；(Ⅱ)过点
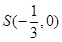的动直线l交椭圆C于A、B两点，试问：在坐标平面上是否存在一个定点T，使得无论l如何转动，以AB为直径的圆恒过点T，若存在，求出点T的坐标；若不存在，请说明理由．