(本小题满分14分)已知函数 (Ⅰ)当
(Ⅰ)当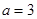 时,求
时,求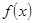 的单调增区间;(Ⅱ)若
的单调增区间;(Ⅱ)若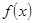 在
在 上是增函数,求
上是增函数,求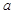 得取值范围;(Ⅲ)
得取值范围;(Ⅲ) 在(Ⅱ)的结论下,设
在(Ⅱ)的结论下,设 ,求函数
,求函数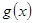 的最小值.
的最小值.
已知直线 在
在 轴上截距相等,且到点
轴上截距相等,且到点 的距离等于
的距离等于 ,求直线
,求直线 的方程.
的方程.
已知数列 的首项
的首项 ,
, ,
, .
.
(1)求 的通项公式;
的通项公式;
(2)证明:对任意的 ,
, ,
, ;
;
(3)证明: .
.
如图,设抛物线方程为 直线
直线 上任意一点,过M引抛物线的切线,切点分别为A,B。
上任意一点,过M引抛物线的切线,切点分别为A,B。
(1)求证:A,M,B三点的横坐标成等差数列;
(2)已知当M点的坐标为 时,
时, ,求此时抛物线的方程;
,求此时抛物线的方程;
(3)是否存在点M,使得点C关于直线AB的对称点D在抛物线 上,其中,点C满足
上,其中,点C满足 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
已知函数 。(1)求函数
。(1)求函数 的单调区间和值域;
的单调区间和值域;
(2)设 ,函数
,函数 ,若对于任意
,若对于任意 总存在
总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围。
的取值范围。
如图,等边 与直角梯形ABDE所在平面垂直,
与直角梯形ABDE所在平面垂直, ,AE⊥AB,
,AE⊥AB, ,O为AB的中点.
,O为AB的中点.
|

 ;
;
 的余弦值.
的余弦值.