(本小题共12分)
已知双曲线 过点A(2,3),其一条渐近线的方程为
过点A(2,3),其一条渐近线的方程为

(I)求该双曲线的方程;
(II)若过点A的直线与双曲线右支交于另一点B,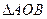 的面积为
的面积为 ,其中O为坐标原点,求直线AB的方程。
,其中O为坐标原点,求直线AB的方程。
(本小题满分12分)如图,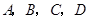 为空间四点.在
为空间四点.在 中,
中,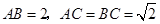 .等边三角形
.等边三角形 以
以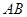 为轴运动.
为轴运动.
(1)当平面 平面
平面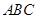 时,求
时,求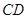 ;
;
(2)当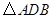 转动时,证明总有
转动时,证明总有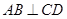 ?
?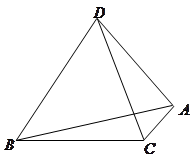
(本小题满分12分)如图,角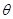 的始边
的始边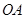 落在
落在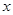 轴上,其始边、终边分别与单位圆交于点
轴上,其始边、终边分别与单位圆交于点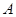 、
、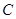 (
(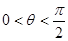 ),△
),△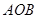 为等边三角形.
为等边三角形.
(1)若点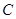 的坐标为
的坐标为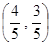 ,求
,求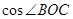 的值;
的值;
(2)设 ,求函数
,求函数 的解析式和值域.
的解析式和值域.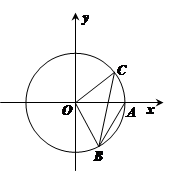
(本小题满分10分)已知函数
(1)试求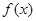 的值域;
的值域;
(2)设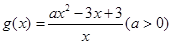 ,若对
,若对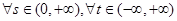 恒有
恒有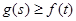 成立,试求实数
成立,试求实数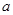 的取值氛围。
的取值氛围。
(本小题满分12分)设函数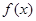 的定义域为R,当
的定义域为R,当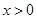 时,
时,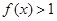 ,且对任意
,且对任意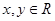 ,都有
,都有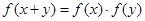 ,且
,且 。
。
(1)求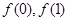 的值;
的值;
(2)证明: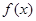 在R上为单调递增函数;
在R上为单调递增函数;
(3)若有不等式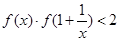 成立,求
成立,求 的取值范围。
的取值范围。
(本小题满分12分)对于定义域为D的函数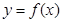 ,若同时满足下列条件:①
,若同时满足下列条件:①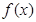 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[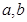 ]
] ,使
,使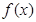 在[
在[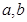 ]上的值域为[
]上的值域为[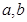 ];那么把
];那么把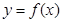 (
(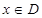 )叫闭函数。(1)求闭函数
)叫闭函数。(1)求闭函数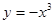 符合条件②的区间[
符合条件②的区间[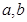 ];
];
(2)判断函数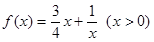 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)判断函数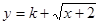 是否为闭函数?若是闭函数,求实数
是否为闭函数?若是闭函数,求实数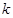 的取值范围。
的取值范围。