(本小题共8分)
已知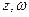 为复数,
为复数, 为纯虚数,
为纯虚数, ,且
,且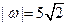 。求复数
。求复数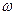 。
。
已知 的图像与
的图像与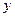 轴的交点为
轴的交点为 ,它在
,它在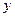 轴右侧的第一个最大值和最小值点分别为
轴右侧的第一个最大值和最小值点分别为 和
和
(1)求 的解析式;
的解析式;
(2)求 的单调递增区间
的单调递增区间
(3)将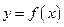 的图像上所有点的横坐标变为原来的
的图像上所有点的横坐标变为原来的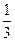 ,再将所得图像向右平移
,再将所得图像向右平移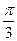 个单位得函数
个单位得函数 的图像,求
的图像,求 的解析式。
的解析式。
为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计。请你根据表中信息解答下列问题:
(1)若用系统抽样的方法抽取容量为50的一个样本,则写出表中的①②③④⑤填的数据;
(2)作出频率分布直方图;
(3)试估计参加这次竞赛的学生的平均成绩
(1)一本300页的书,随机打开一页,求页码在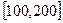 之间的概率。
之间的概率。
(2)在区间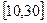 内的所有实数中,随机地取一个实数
内的所有实数中,随机地取一个实数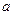 ,求实数
,求实数 的概率
的概率
已知 的3个顶点为
的3个顶点为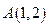 ,
, ,
, (1)求
(1)求 的值;
的值;
(2)求 的大小,并判断
的大小,并判断 的形状。
的形状。
(本小题16分)
首项为正数的数列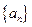 满足
满足


(I)证明:若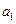 为奇数,则对一切
为奇数,则对一切 都是奇数;
都是奇数;
(II)若对一切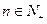 都有
都有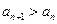 ,求
,求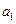 的取值范围.
的取值范围.