(本小题10分)
某工厂生产某种产品,已知该产品的月产量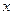 (吨)与每吨产品的价格
(吨)与每吨产品的价格 (元/吨)之间的关系为
(元/吨)之间的关系为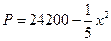 ,且生产
,且生产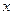 吨产品的成本为
吨产品的成本为 (元)。问该工厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?
(元)。问该工厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?
将正整数按如图的规律排列,把第一行数1,2,5,10,17, 记为数列 ,第一
,第一
数列1,4,9,16,25, 记为数列

(1)写出数列 ,
, 的通项公式;
的通项公式;
(2)若数列 ,
, 的前n项和分别为
的前n项和分别为 ,用数学归纳法证明:
,用数学归纳法证明: ;
;
(3)当 时,证明:
时,证明: .
.
已知 ,
, ,且
,且 ,
, 在
在 和
和 处有极值.
处有极值.
(1)求实数 的值;
的值;
(2)若 ,判断
,判断 在区间
在区间 内的单调性.
内的单调性.
抽奖游戏规则如下:一个口袋中装有完全一样的8个球,其中4个球上写有数字“5”,另外4个球上写有数字“10”.
(1)每次摸出一个球,记下球上的数字后放回,求抽奖者四次摸球数字之和为30的概率;
(2)若抽奖者每交2元钱(抽奖成本)获得一次抽奖机会,每次摸出4个球,若4个球数字之和为20或40则中一等奖,奖励价值20元的商品一件;若4个球数字之和为25或35则中二等奖,奖励价值2元的商品一件;若4个球数字之和为30则不中奖.试求抽奖者收益ξ(奖品价值﹣抽奖成本)的期望.
偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,在某次考试成绩统计中,某老师为了对学生数学偏差 (单位:分)与物理偏差
(单位:分)与物理偏差 (单位:分)之间的关系进行分析,随机挑选了8位同学,得到他们的两科成绩偏差数据如下:
(单位:分)之间的关系进行分析,随机挑选了8位同学,得到他们的两科成绩偏差数据如下:
| 学生序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
数学偏差 |
20 |
15 |
13 |
3 |
2 |
﹣5 |
﹣10 |
﹣18 |
物理偏差 |
6.5 |
3.5 |
3.5 |
1.5 |
0.5 |
﹣0.5 |
﹣2.5 |
﹣3.5 |
(1)若 与
与 之间具有线性相关关系,求y关于x的线性回归方程;
之间具有线性相关关系,求y关于x的线性回归方程;
(2)若该次考试该班数学平均分为120分,物理平均分为91.5分,试由(1)的结论预测数学成绩为128分的同学的物理成绩.
参考数据:

已知函数 的图象上一点
的图象上一点 ,过
,过 作平行于
作平行于 轴的直线
轴的直线 ,直线
,直线 ,求函数
,求函数 ,
, 和
和 轴,及直线
轴,及直线 轴围成的面积
轴围成的面积