将一个质地均匀的正方体骰子连续抛掷3次,它落地时向上的点数依次成等差数列的概率为( )
A.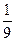 |
B.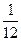 |
C. |
D.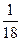 |
.设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)> 0,且g(-3)=0,则不等式f(x)g(x)<0的解集是( )
| A.(-3,0)∪(3,+∞) |
| B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) |
| D.(-∞,-3)∪(0,3) |
用数学归纳法证明“42n-1+3n+1(n∈N*)能被13整除”的第二步中,当n=k+1时为了使用归纳假设,对42k+1+3k+2变形正确的是( )
| A.16(42k-1+3k+1)-13×3k+1 |
| B.4×42k+9×3k |
| C.(42k-1+3k+1)+15×42k-1+2×3k+1 |
| D.3(42k-1+3k+1)-13×42k-1 |
甲、乙、丙等五人站成一排,要求甲、乙均不与丙相邻,则不同的排法为()
| A.72 | B.36 | C.52 | D.24 |
已知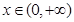 有下列各式:
有下列各式: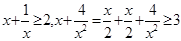 ,
,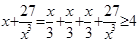 成立,观察上面各式,按此规律若
成立,观察上面各式,按此规律若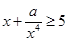 ,则正数
,则正数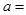 ()
()
| A.4 | B.5 | C.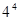 |
D.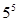 |
若a、b∈R,且ab>0,则下列不等式中,恒成立的是()
| A.a2+b2>2ab | B.a+b≥2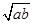 |
C.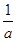 + +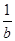 > >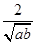 |
D. + +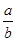 ≥2 ≥2 |