选修4—1：（本小题满分10分）几何证明选讲
如图，在△ABC中，∠C为钝角，点E，
H分别是边AB上的点，点K和M分别
是边AC和BC上的点，且AH＝AC，EB
＝BC，AE＝AK，BH＝BM．
（Ⅰ）求证：E、H、M、K四点共圆；
（Ⅱ）若KE＝EH，CE＝3，求线段KM的
长．
在直角梯形P1DCB中，P1D//CB，CD//P1D且P1D = 6，BC = 3，DC =
，A是P1D的中点，沿AB把平面P1AB折起到平面PAB的位置，使二面角P－CD－B成45°角，设E、F分别是线段AB、PD的中点．
（1）求证：AF//平面PEC；
（2）求平面PEC和平面PAD所成的二面角的大小；
（3）求点D到平面PEC的距离．
目前高中毕业会考中，成绩在85～100为“A”,70～84为“B”,60～69为“C”,60分以下为“D”.编制程序，输入学生的考试成绩(百分制，若有小数则四舍五入)，输出相应的等级.
对某400件元件进行寿命追踪调查情况频率分布如下:
| 寿命(h) |
频率 |
| 500～600 |
0.10 |
| 600～700 |
0.15 |
| 700～800 |
0.40 |
| 800～900 |
0.20 |
| 900～1000 |
0.15 |
| 合计 |
1 |
(1)估计元件寿命在500～800 h以内的频率；
(2)估计元件寿命在800 h以上的频率.
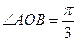
（1）P, Q中点M的轨迹方程；
（2）
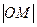的最小值。
