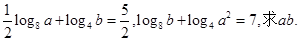（本小题满分1
2分）
某市举行一次数学新课程骨干培训，共邀请15名使用不同版本教材的教师，数据如下表所示：
| 版本 |
人教A版 |
人教B版 |
||
| 性别 |
男教师 |
女教师 |
男教师 |
女教师 |
| 人数 |
6 |
3 |
4 |
2 |
(1)从这15名教师中随机选出2名，则2人恰好是教不同版本的男教师的概率是多少？
(2)培训活动随机选出2名代表发言，设发言代表中使用人教B版的女教师人数为
，求随机变量的分布列和数学期望
.
已知函数y=
(a2x)·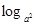
(
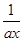)(2≤x≤4)的最大值为0，最小值为－
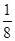，求a的值.
已知函数f（x）=3x+k（k为常数），A（－2k，2）是函数y= f－1（x）图象上的点.
（1）求实数k的值及函数f－1（x）的解析式；
（2）将y= f－1（x）的图象按向量a=（3，0）平移，得到函数y=g（x）的图象，若2 f－1（x+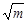
－3）－g（x）≥1恒成立，试求实数m的取值范围.
若f（x）=x2－x+b，且f（log2a）=b，log2［f（a）］=2（a≠1）.
（1）求f（log2x）的最小值及对应的x值；
（2）x取何值时，f（log2x）＞f（1）且log2［f（x）］＜f（1）？
甲、乙两人解关于
的方程：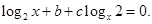
甲写错了常数b，得到根为
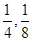，乙写错了常数c，得到根为
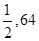.求方程的真正根。
已知