(本小题满分12分）
某电视台为了宣传某沿江城市经济崛起的情况，特举办了一期有奖知识问答活动，活动对18—48岁的人群随机抽取 n人回答问题“沿江城市带包括哪几个城市”，统计数据结果如下表：
| 组数 |
分组 |
回答正 确的人数 |
占本组 的频率 |
| 第1组 |
[18，28〕 |
240 |
X |
| 第2组 |
[28，38〕 |
300 |
0.6 |
| 第3组 |
[38，48〕 |
a |
0.4 |
（Ⅰ）分别求出n,a,x的值;
（Ⅱ）若以表中的频率近似看作各年龄组正确回答问题的概率,规定年龄在[38,48〕内回答正确的得奖金200元,年龄在[18,28〕内回答正确的得奖金100元。主持人随机请一家庭的两个成员(父亲46岁,孩子21岁)回答正确,求该家庭获得奖金
的分布列及数学期望(两人回答问题正确与否相互独立)。
本小题满分14分）
在△ABC中，角A，B，C所对的边分别为a，b，c，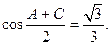
（I）求
的值；
（II）若
的值.
、(本小题满分16分)
已知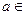
R，函数
R，
为自然对数的底数)。
(1)当
时，求函数
的单调递增区间；
(2)若函数在
上单调递增，求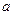
的取值范围；
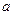(3)函数是否为R上的单调函数，若是，求出的取值范围；若不是，请说明理由。
、(本小题满分14分)
设函数
，其中实常数
。
(1)求函数
的定义域和值域；
(2)试探究函数的奇偶性与单调性，并证明你的结论。
、(本小
题满分14分)
已知函数
(1)画出函数在
的简图；
(2)写出函数的最小正周期和单调递增区间；并求：当x为何值时，函数有最大值？最大值是多少？
(3)若x是△ABC的一个内角，且y2＝1，试判断△ABC的形状。
、(本小题满分14分)
在平面直角坐标系xoy中，点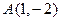
、
、
。
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长；
(2)设实数t满足
，求t的值。