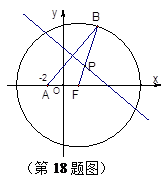
已知函数
(1)求曲线 在点
在点 处的切线方程
处的切线方程
(2)当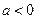 时,求函数
时,求函数 的单调区间
的单调区间
如图6,在三棱柱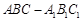 中,△ABC为等边三角形,侧棱
中,△ABC为等边三角形,侧棱 ⊥平面
⊥平面 ,
,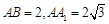 ,D、E分别为
,D、E分别为 、
、 的中点.
的中点.
(Ⅰ)求证:DE⊥平面 ;
;
(Ⅱ)求BC与平面 所成角;
所成角;
(Ⅲ)求三棱锥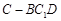 的体积.
的体积.
甲、乙两人各掷一颗质地均匀的骰子,如果所得它们向上的点数之和为偶数,则甲赢,否则乙赢.
(Ⅰ)求两个骰子向上点数之和为8的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?试说明理由
如图5,已知平面 ∩平面
∩平面 =AB,PQ⊥
=AB,PQ⊥ 于Q,PC⊥
于Q,PC⊥ 于C,CD⊥
于C,CD⊥ 于D.
于D.
(Ⅰ)求证:P、C、D、Q四点共面;
(Ⅱ)求证:QD⊥AB.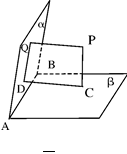
甲、乙两人同时生产一种产品,6天中,完成的产量茎叶图(茎表示十位,叶表示个位)如图所示:
(Ⅰ)写出甲、乙的众数和中位数;
(Ⅱ)计算甲、乙的平均数和方差,依此判断谁更优秀?
已知定点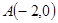 ,动点
,动点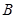 是圆
是圆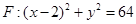 (
(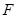 为圆心)上一点,线段
为圆心)上一点,线段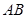 的垂直平分线交
的垂直平分线交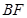 于点
于点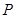 .
.
(I)求动点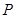 的轨迹方程;
的轨迹方程;
(II)是否存在过点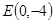 的直线
的直线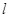 交
交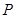 点的轨迹于点
点的轨迹于点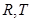 ,且满足
,且满足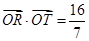 (
(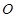 为原点).若存在,求直线
为原点).若存在,求直线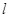 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.