已知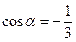 ,
,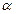 为第二象限角,求
为第二象限角,求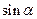 和
和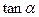 及
及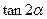 的值.
的值.
如图,在三棱锥 中,侧面
中,侧面 与侧面
与侧面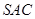 均为等边三角形,
均为等边三角形, ,
,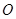 为
为 中点.
中点.
(Ⅰ)证明: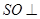 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
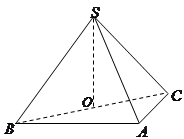
盒中有6只灯泡,其中2只次品,4只正品,有放回地从中任取两次,每次取一只,试求下列事件的概率:(1)取到的2只都是次品;(2)取到的2只中正品、次品各一只;
(3)取到的2只中至少有一只正品.
已知在 中,
中, 所对的边分别为
所对的边分别为 ,若
,若 且
且 .
.
(Ⅰ)求角A、B、C的大小;
(Ⅱ)设函数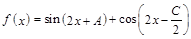 ,求函数
,求函数 的单调递增区间,并指出它相邻两对称轴间的距离.
的单调递增区间,并指出它相邻两对称轴间的距离.
已知函数 ,
,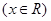 .
.
(1)求函数 的单调区间和极值;
的单调区间和极值;
(2)已知函数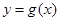 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称;
对称;
证明:当 时,
时,
(3)如果 且
且 ,证明
,证明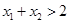
设 .
.
(1)求实数a;
(2)求数列{xn}的通项公式;
|
(3)若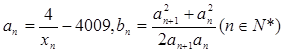 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.