(本小题满分12分)
已知某种产品共有6个,其中有2个不合格产品,质检人员从中随机抽出2个,
(1) 抽取 产品中只有一个合格产品的概率是多少?
产品中只有一个合格产品的概率是多少?
(2) 检测出不合格产品的概率是多少?
已知集合A={x|x=a2+1,a∈N*},B={y|y=b2-4b+5,b∈N*},证明A B.
B.
设集合A={x|-1<x<2},B={x|4px+1<0},试判断A、B之间能否存在某种包含关系?若存在,找出p的取值范围,并指明对应的包含关系;若不存在,证说明理由.
设集合A=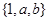 ,B=
,B=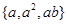 ,且A=B,求实数
,且A=B,求实数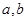 的值.
的值.
已知集合A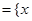 ,
,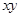 ,
,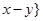 ,集合B={0,|x|,y},
,集合B={0,|x|,y},
(1)若A=B,求实数x、y的值;
(2)是否存在实数x、y使得A与B是不相等的两个集合,但它们都有以0为其中的一个元素的相同的子集?试指出存在条件或不存在的理由.
集合A={x|ax2-2x+1="0},B={x|" x2-2x+a=0}中,已知A只有一个元素,求集合A与B .