图15为“双聚焦分析器”质谱仪的结构示意图，其中，加速电场的电压为U，静电分析器中与圆心O1等距离的各点场强大小相等、方向沿径向，磁分析器中以O2为圆心、圆心角为90°的扇形区域内，分布着方向垂直于纸面的匀强磁场，其左边界与静电分析器的右端面平行.由离子源发出的一质量为m、电荷量为q的正离子(初速度为零，重力不计）经加速电场加速后，从M点垂直于电场方向进入静电分析器，沿半径为R的四分之一圆弧轨迹做匀速圆周运动，从N点射出，接着由P点垂直磁分析器的左边界射入，最后垂直
于下边界从Q点射出并进入收集器.已知Q点与圆心O2的距离为么求：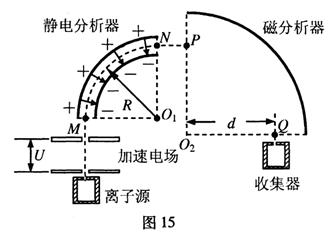
(1) 磁分析器中磁场的磁感应强度B的大小和方向；
(2) 静电分析器中离子运动轨迹处电场强度E的大小；
(3) 现将离子换成质量为0.9m、电荷量仍为q的另一种正离子，其它条件不变.试直接指出该离子进入磁分析器时的位置，它射出磁场的位置在Q点的左侧还是右侧？
(18分)用一根长20cm，劲度系数k=200N/m的弹簧水平拉着放在水平桌面上质量为1kg的木块，弹簧的长度逐渐伸长到22.4ｃｍ时开始运动，当弹簧的长度为21.7ｃｍ时，木块在桌面上做匀速运动。
（1）木块受到的最大静摩擦力多大？静摩擦的变化范围怎样？
（2）木块与桌面间的动摩擦因数是多少？
（3）木块滑动的过程中，当弹簧的长度小于或大于21.7ｃｍ时，滑动摩擦力如何变化？（ｇ＝１０Ｎ／ｋｇ）
(18分) 一个小球在光滑水平面上运动的v—t图象如图所示。求：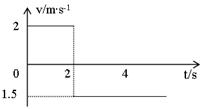
（1）试描述小球的运动情况？
（2）画出前5s小球运动的s—t图象？
（3）5s内小球运动的位移？
如图甲所示，质量为M＝3.0kg的平板小车C静止在光滑的水平面上，在t＝0时，两个质量均为1.0kg的小物体A和B同时从左右两端水平冲上小车，1.0s内它们的v—t图象如图乙所示，g取10m/s2.
（1）小车在第1.0s内所受的合力为多大？
（2）要使A、B在整个运动过程中不会相碰，车的长度至少为多少？
（3）假设A、B两物体在运动过程中不会相碰，试在图乙中画出A、B在t=1.0s～3.0s时间内的v—t图象．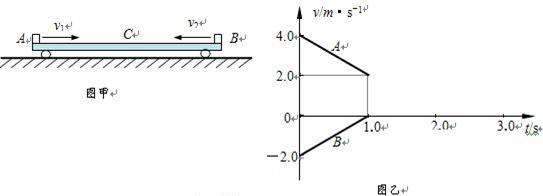
（10分)如图，已知斜面倾角300，物体A质量mA=0.4kg，物体B质量mB=0.7kg，H=0.5m。B从静止开始和A一起运动，B落地时速度v=2m/s。若g取10m/s2，绳的质量及绳的摩擦不计，求：
（1）物体与斜面间的动摩擦因数
（2）物体沿足够长的斜面滑动的最大距离
如右图所示，两个完全相同的物块，重力大小为G，两球与水平面的动摩擦因数都为μ，一根轻绳两端固定在两小球上，在绳的中点施加一个竖直向上的拉力，当绳子被拉直后，两段绳的夹角为α，问当F至少为多大，两物块将会发生滑动？（设物块受到的最大静摩擦力等于滑动摩擦力）