如图,某学校要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用一种颜色的鲜花,相邻区域使用不同颜色的鲜花,现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择。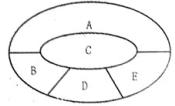
(I)求恰有两个区域用红色鲜花的概率;
(II)记ξ为花圃中用红色鲜花布置区域个数,求随机变量ξ的分布列及其数学期望Eξ.
已知函数f1(x)=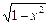 ,f2(x)=x+2,
,f2(x)=x+2,
(1)设y=f(x)=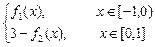 ,试画出y=f(x)的图像并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积;
,试画出y=f(x)的图像并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积;
(2)若方程f1(x+a)=f2(x)有两个不等的实根,求实数a的范围.
(3)若f1(x)>f2(x-b)的解集为[-1,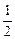 ],求b的值.
],求b的值.
已知函数f(x)是y=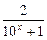 -1(x∈R)的反函数,函数g(x)的图像
-1(x∈R)的反函数,函数g(x)的图像
与函数y=-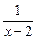 的图像关于y轴对称,设F(x)=f(x)+g(x).
的图像关于y轴对称,设F(x)=f(x)+g(x).
(1)求函数F(x)的解析式及定义域;
(2)试问在函数F(x)的图像上是否存在两个不同的点A、B,使直线AB恰好与y轴垂直?若存在,求出A、B的坐标;若不存在,说明理由
如图,函数y= |x|在x∈[-1,1]的图像上有两点A、B,AB∥Ox轴,点M(1,m)(m∈R且m>
|x|在x∈[-1,1]的图像上有两点A、B,AB∥Ox轴,点M(1,m)(m∈R且m> )是△ABC的BC边的中点.
)是△ABC的BC边的中点.
(1)写出用B点横坐标t表示△ABC面积S的函数解析式S=f(t);
(2)求函数S=f(t)的最大值,并求出相应的C点坐标.
设不等式2(log x)2+9(log
x)2+9(log x)+9≤0的解集为M,求当x∈M时函数f(x)=(log2
x)+9≤0的解集为M,求当x∈M时函数f(x)=(log2 )(log2
)(log2 )的最大、最小值.
)的最大、最小值.
已知函数x,y满足x≥1,y≥1 loga2x+loga2y=loga(ax2)+loga(ay2)(a>0且a≠1),求loga(xy)的取值范围.
loga2x+loga2y=loga(ax2)+loga(ay2)(a>0且a≠1),求loga(xy)的取值范围.