某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被考官A面试的概率?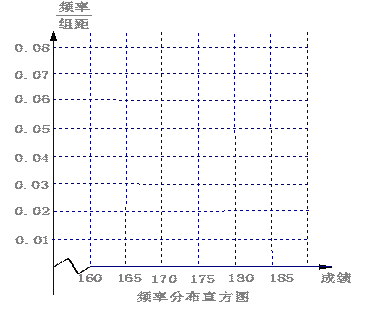
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
 |
5 |
0.050 |
| 第2组 |
 |
① |
0.350 |
| 第3组 |
 |
30 |
② |
| 第4组 |
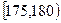 |
20 |
0.200 |
| 第5组 |
 |
10 |
0.100 |
| 合计 |
100 |
1.000 |
|
汶川震后在社会各界的支持和帮助下,汶川一中临时搭建了学校,学校餐厅也做到了保证每天供应1000名学生用餐,每星期一有A、B两样菜可供选择(每个学生都将从二者中选一),为了让学生们能够安心上课对学生的用餐情况进行了调查。调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A 、B
、B 分别表示在第n个星期一选A、B菜的人数。
分别表示在第n个星期一选A、B菜的人数。
(1)试以A 表示A
表示A ;
;
(2)若A =200,求{A
=200,求{A }的通项公式;
}的通项公式;
(3)问第n个星期一时,选A与选B的人数相等?
已知向量 ,
,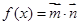 .
.
(I)若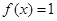 ,求
,求 值;
值;
(II)在 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求函数
,求函数 的取值范围.
的取值范围.
已知奇函数
(1)试确定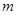 的值;
的值;
(2)若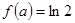 ,求
,求 的值;
的值;
(3)求函数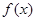 在
在 上的最小值.
上的最小值.
经过调查发现,某一时尚产品在投放市场的30天中,前20天其价格呈直线上升,后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示:
| 时间 |
第4天 |
第12天 |
第21天 |
第28天 |
| 价格(百元) |
34 |
42 |
48 |
34 |
(1)写出价格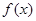 关于时间
关于时间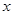 的函数表达式(
的函数表达式(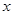 表示投放市场的第
表示投放市场的第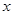 天);
天);
(2)若销售量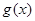 与时间
与时间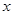 的函数关系式为:
的函数关系式为: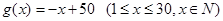 ,问该产品投放市场第几天,日销售额最高?
,问该产品投放市场第几天,日销售额最高?
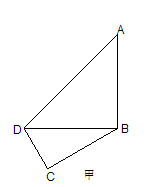
如图甲,在平面四边形ABCD中,已知
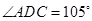 ,
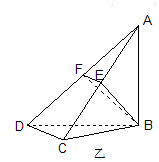
,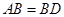 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD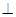 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
(Ⅰ)求证:DC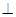 平面ABC;
平面ABC;
(Ⅱ)设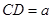 ,求三棱锥F-ABE的体积.
,求三棱锥F-ABE的体积.