汶川震后在社会各界的支持和帮助下，汶川一中临时搭建了学校，学校餐厅也做到了保证每天供应1000名学生用餐，每星期一有A、B两样菜可供选择（每个学生都将从二者中选一），为了让学生们能够安心上课对学生的用餐情况进行了调查。调查资料表明，凡是在本周星期一选A菜的，下周星期一会有20％改选B，而选B菜的，下周星期一则有30％改选A，若用A
、B分别表示在第n个星期一选A、B菜的人数。
（1）试以A表示A
；
（2）若A
=200，求{A}的通项公式；
（3）问第n个星期一时，选A与选B的人数相等？
（本小题满分16分）函数
其中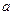
为常数，且函数
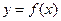和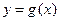
的图像在其与坐标轴的交点处的切线互相平行
（1）、求函数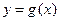的解析式
（2）、若关于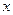
的不等式
恒成立，求实数
的取值范围。
已知椭圆
的离心率为
，直线
:
与以原点为圆心、以椭圆
的短半轴长为半径的圆相切.
（I）求椭圆的方程；
（II）设椭圆的左焦点为
，右焦点
，直线
过点且垂直于椭圆的长轴，动直线
垂直于点
，线段
垂直平分线交于点
，求点的轨迹
的方程；
（III）设与
轴交于点
，不同的两点
在上，且满足
求
的取值范围.
（本小题满分12分）
已知数列
满足
（1）求
；
（2）已知存在实数
，使
为公差为
的等差数列，求的值；
（3）记
，数列
的前
项和为
，求证：
.
（本小题满分12分）
|
已知点A是抛物线y2＝2px（p>0）上一点，F为抛物线的焦点，准线l与x轴交于点K，已知｜AK｜＝
｜AF｜，三角形AFK的面积等于8．
（本小题满分13分）如图，在矩形ABCD中，已知A（2，0）、C（－2，2），点P在BC边上移动，线段OP的垂直平分线交y轴于点E，点M满足
（Ⅰ）求点M的轨迹方程；
（Ⅱ）已知点F（0，
），过点F的直线l交点M的轨迹于Q、R两点，且
求实数
的取值范围.