、已知关于x的一元二次函数 ,设集合
,设集合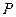 ={1,2,3},
={1,2,3},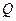 ={-1,1,2,3,4,},分别从集合
={-1,1,2,3,4,},分别从集合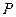 和
和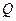 中随机取一个数作为
中随机取一个数作为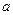 和
和 .
.
(1)求函数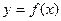 有零点的概率;
有零点的概率;
(2)求函数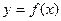 在区间[1,+∞)上是增函数的概率.
在区间[1,+∞)上是增函数的概率.
(本题满分10分)
已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求 在
在 上的最大值和最小值.
上的最大值和最小值.
椭圆的两焦点坐标分别为F1( ,0),F2(
,0),F2(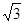 ,0),且椭圆过点P(1,
,0),且椭圆过点P(1, ).
).
(1)求椭圆方程;
(2)若 A为椭圆的左顶点,作AM⊥AN与椭圆交于两点M、N,试问:直线MN是否恒过x轴上的一个定点?若是,求出该点坐标;若不是,请说明理由.
若椭圆C1: 的离心率等于
的离心率等于 ,抛物线C2:x2=2py(p>0)的焦点是椭圆C1的一个顶点.
,抛物线C2:x2=2py(p>0)的焦点是椭圆C1的一个顶点.
(1)求抛物线C2的方程;
(2)若过M(-1,0)的直线l与抛物线C2交于E、F两点,又过E、F作抛物线C2的切线l1、l2,当l1⊥l2时,求直线l的方程.
已知二次函数y=f(x)的图象经过坐标原点,其导函数f ′(x)=2x+2,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设bn=2n·an,Tn是数列{bn}的前n项和,求Tn.
在△ABC中,a、b、c分别是角A、B、C的对边,向量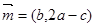 ,
,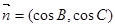 ,且
,且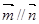
(1)求角B的大小;
(2)设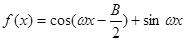 (
( ),且f(x)的最小正周期为π,求f(x)的单调区间.
),且f(x)的最小正周期为π,求f(x)的单调区间.