(本小题满分12分)
如图,棱锥P—ABCD的底面ABCD是矩形,
PA⊥平面ABCD,PA=AD=2, BD=
BD=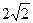 .
.
(1)求点C到平面PBD的距离.
|
(2)在线段 上是否存在一点
上是否存在一点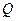 ,使
,使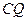 与平面
与平面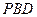 所成的角
所成的角
 ,若存在,指出点
,若存在,指出点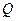 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
200辆汽车通过某一路段时时速频率分布直方图如图2-2-9所示,则时速在[50,60]的汽车大约有______辆.
图2-2-9
有一个简单的随机样本:10, 12, 9, 14, 13,则样本平均数 =______,样本方差
=______,样本方差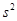 =______。
=______。
体某村有旱地与水田若干,现需要估计平均亩产量.如果按5%分层抽样的方法抽取15亩旱地、45亩水田进行调查,则这个村的旱地与水田的亩数分别为__________,___________.
下列结论不正确的是(填序号).
①各个面都是三角形的几何体是三棱锥
②以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥
③棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥
④圆锥的顶点与底面圆周上的任意一点的连线都是母线
对任意实数x,y,定义运算 ,其中
,其中 为常数,等号右边的运算是通常意义的加乘运算,现已知
为常数,等号右边的运算是通常意义的加乘运算,现已知 ,
, ,且有一个非零实数m,使得对任意实数x,都有
,且有一个非零实数m,使得对任意实数x,都有 ,则
,则 ______________。
______________。