(本小题满分12分)
已知数列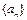 的首项
的首项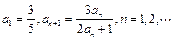 .
.
(Ⅰ)求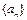 的通项公式;
的通项公式;
(Ⅱ)证明:对任意的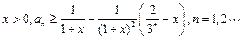 ;
;
(Ⅲ)证明: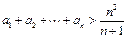 .
.
如图,A、B是海面上位于东西方向相距5(3+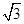 )海里的两个观测点,现位于A点北偏东45°、B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°、B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20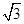 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到D点需要多长时间?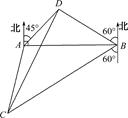
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
某人在汽车站M的北偏西20°的方向上的A处(如图所示),观察到C处有一辆汽车沿公路向M站行驶,公路的走向是M站的北偏东40°.开始时,汽车到A处的距离为31km,汽车前进20km后,到A处的距离缩短了10km.问汽车还需行驶多远,才能到达汽车站M?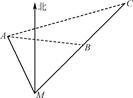
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2h追上,此时到达C处.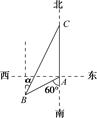
(1)求渔船甲的速度;
(2)求sinα的值.
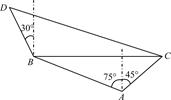
在海岸A处,发现北偏西75°的方向,距离A2海里的B处有一艘走私船,在A处北偏东45°方向,距离A( -1)海里的C处的缉私船奉命以10
-1)海里的C处的缉私船奉命以10 海里/小时的速度追截走私船.此时,走私船正以10海里/小时的速度从B向北偏西30°方向逃窜,问缉私船沿什么方向能最快追上走私船?
海里/小时的速度追截走私船.此时,走私船正以10海里/小时的速度从B向北偏西30°方向逃窜,问缉私船沿什么方向能最快追上走私船?