(本小题满分13分)
如图,已知正三棱柱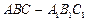 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是 的中点,直线
的中点,直线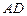 与侧面
与侧面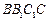 所成的角是
所成的角是 .
.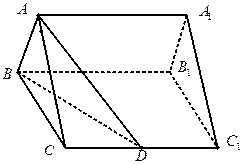
⑴求二面角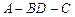 的大小;
的大小;
⑵求点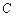 到平面
到平面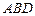 的距离.
的距离.
(本小题满分13分)
已知函数 是定义在
是定义在 上的奇函数.
上的奇函数.
(Ⅰ)求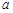 的值;
的值;
(Ⅱ)求函数 的值域;
的值域;
(Ⅲ)当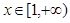 时,
时,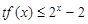 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分13分)
专家通过研究学生的学习行为,发现学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设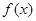 表示学生注意力随时间
表示学生注意力随时间 (分钟)的变化规律(
(分钟)的变化规律(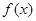 越大,表明学生注意力越大),经过试验分析得知:
越大,表明学生注意力越大),经过试验分析得知:
(Ⅰ)讲课开始后多少分钟,学生的注意力最集中?能坚持多少分钟?
(Ⅱ)讲课开始后5分钟时与讲课开始后25分钟时比较,何时学生的注意力更集中?
(Ⅲ)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲完这道题目?
(本小题满分12分)
为了了解小学五年级学生的体能情况,抽取了实验小学五年级部分学生进行踢毽子测试,将所得的数据整理后画出频率分布直方图(如图),已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数是5.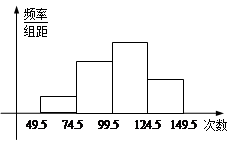
(Ⅰ)求第四小组的频率和参加这次测试的学生人数;
(Ⅱ)在这次测试中,问学生踢毽子次数的中位数落在第几小组内?
(Ⅲ)在这次跳绳测试中,规定跳绳次数在110以上的为优秀,试估计该校此年级跳绳成绩的优秀率是多少?
(本小题满分12分)
朵朵小朋友用红、黄、蓝三种颜色的彩笔给下列三个图形随机涂色,每个图形只涂一种颜色,求:


(Ⅰ)三个图形颜色不全相同的概率;
(Ⅱ)三个图形颜色恰有两个相同的概率.
(本小题满分12分)
设函数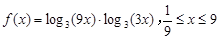 .
.
(Ⅰ)若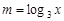 ,求
,求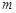 取值范围;
取值范围;
(Ⅱ)求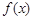 的最值,并给出最值时对应的
的最值,并给出最值时对应的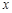 的值.
的值.