如图1，在多面体ABCD—A1B1C1D1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，侧棱延长后相交于E，F两点，上、下底面矩形的长、宽分别为c，d与a，b，且a＞c，b＞d，两底面间的距离为h。
（Ⅰ）求侧面ABB1A1与底面ABCD所成二面角的大小；
（Ⅱ）证明：EF∥面ABCD；
（Ⅲ）在估测该多面体的体积时，经常运用近似公式V估=S中截面·h来计算.已知它的体积公式是V=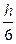
（S上底面+4S中截面+S下底面），试判断V估与V的大小关系，并加以证明。
（注：与两个底面平行，且到两个底面距离相等的截面称为该多面体的中截面）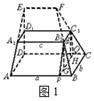
如图所示，在四棱锥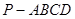
中，底面ABCD是边长为a的正方形，侧面
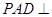底面ABCD，且
，若E，F分别为PC，BD的中点．
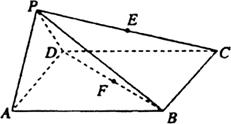
（1）求证：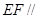
平面PAD；
（2）求证：平面PDC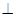
平面PAD；
（3）求四棱锥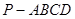的体积．
设函数
（1）写出函数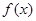
的最小正周期及单调递减区间；
（2）当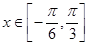
时，函数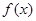的最大值与最小值的和为
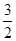，求不等式
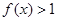的解集．
设关于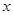
的一元二次方程
.
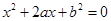（1）若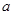
，
都是从集合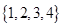
中任取的数字，求方程有实根的概率；
（2）若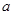是从区间[0,4]中任取的数字，是从区间[1，4]中任取的数字，求方程有实根的概率．
已知数列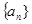
的前n项和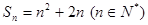
．
（1）求数列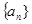的通项公式；
（2）若数列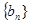
是等比数列，公比为
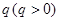，且满足
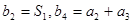，求数列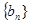的前n项和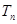
．
(本题满分10分)选修4 - 5 ：不等式选讲
设函数，
.
(I)求证
；
(II)若
成立，求x的取值范围.