抛掷两颗骰子,求:
(Ⅰ)点数之和出现7点的概率;(Ⅱ)出现两个4点的概率.
(本小题满分14分)设函数f(x)=(x–1)2+alnx,a∈R.
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线与直线x+2y–1=0垂直,求a的值;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若函数f(x)有两个极值点x1,x2且x1<x2,求证:f(x2)> –
– ln2.
ln2.
(本小题满分14分)已知椭圆C: (a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为
(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为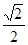 b.
b.
(Ⅰ)求椭圆C的离心率;
(Ⅱ)设b=2,直线y=kx+4与椭圆C交于不同的两点M,N,求证:直线BM与直线AN的交点G在定直线上.
(本小题满分13分)设数列{an}满足:a1=1,an+1=3an,n∈N*.设Sn为数列{bn}的前n项和,已知b1≠0,2bn–b1=S1•Sn,n∈N*.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=bn•log3an,求数列{cn}的前n项和Tn.
(本小题满分14分)如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,PC=AB=2AD=2CD=2,E是PB的中点.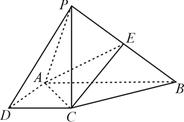
(Ⅰ)求证:平面EAC⊥平面PBC;
(Ⅱ)求二面角P-AC-E的余弦值;
(Ⅲ)求直线PA与平面EAC所成角的正弦值.
(本小题满分13分)在非等腰△ABC中,a,b,c分别是三个内角A,B,C的对边,且a=3,c=4,C=2A.
(Ⅰ)求cosA及b的值;
(Ⅱ)求cos( –2A)的值.
–2A)的值.