(本小题满分12分)
如图:已知△PAB所在的平面与菱形ABCD所在的平面垂直,且PA=PB=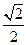 AB,∠ABC=60°,E为AB的中点.
AB,∠ABC=60°,E为AB的中点. 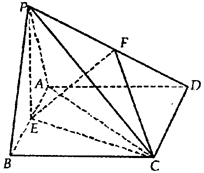
(Ⅰ)证明:CE⊥PA;
(Ⅱ)若F为线段PD上的点,且EF与平面PEC的
夹角为45°,求平面EFC与平面PBC夹角的
余弦值.
(本小题满分14分)已知数列{an}是等差数列,{bn}是等比数列,且满足a1+a2+a3=9,b1b2b3=27.若a4=b3,b4-b3=m.
(1)当m=18时,求数列{an}和{bn}的通项公式;
(2)若数列{bn}是唯一的,求m的值.
(本小题满分14分)如图,在四面体 中,
中, ,点
,点 是
是 的中点,点
的中点,点 在线段
在线段 上,且
上,且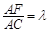 .
.
(1)若 ∥平面
∥平面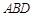 ,求实数
,求实数 的值;
的值;
(2)求证:平面 平面
平面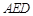 .
.
(本小题满分14分)
已知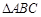 的三个内角
的三个内角 所对的边分别为
所对的边分别为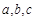 ,向量
,向量 ,
, ,且
,且 .
.
(1)求角A的大小;
(2)若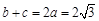 ,求证:
,求证: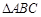 为等边三角形.
为等边三角形.
已知实数 ,函数
,函数 .
.
(1)当 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)若 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)若当 时,函数
时,函数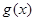 图象上的点均在不等式
图象上的点均在不等式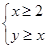 ,所表示的平面区域内,求实数
,所表示的平面区域内,求实数 的取值范围.
的取值范围.
(本小题16分)已知数列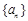 的各项均为正数,数列
的各项均为正数,数列 ,
, 满足
满足 ,
, .
.
(1)若数列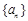 为等比数列,求证:数列
为等比数列,求证:数列 为等比数列;
为等比数列;
(2)若数列 为等比数列,且
为等比数列,且 ,求证:数列
,求证:数列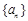 为等比数列.
为等比数列.