（本小题满分12分）
某房地产开发商投资8
1万元建一座写字楼，第一年装修费为1万元，以后每年增加2万元，把写字楼出租，每年收入租金30万元．
（Ⅰ）若扣除投资和各种装修费，则从第几年开始获取纯利润？
（Ⅱ）若干年后开发商为了投资其他项目，有两种处理方案：①年平均利润最大时以46万元出售该楼; ②纯利润总和最大时，以10万元出售该楼，问哪种方案盈利更多？
已知椭圆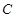
:
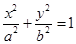
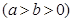的离心率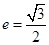
,原点到过点
,
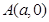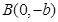的直线的距离是
.
（1）求椭圆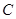
的方程；
（2）若椭圆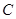上一动点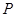
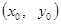关于直线
的对称点为
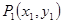，求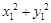
的取值范围；
（3）如果直线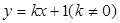
交椭圆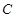于不同的两点
，
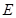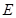，且，都在以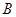
为圆心的圆上，求
的值.
设函数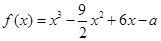
．
（1）对于任意实数
，
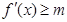恒成立，求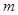
的最大值；
（2）若方程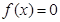
有且仅有一个实根，求
的取值范围．
某市准备从5名报名者（其中男3人，女2人）中选2人参加两个副局长职务竞选.
（1）求所选2人均为女副局长的概率；
（2）若选派两个副局长依次到A、B两个局上任，求A局是男副局长的情况下，B局是女副局长的概率.
为了解高二某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为
.
（1）请将上面的列联表补充完整；
（2）是否有99.5%的把握认为喜爱打篮球与性别有关？说明你的理由；
下面的临界值表供参考：
(参考公式K2＝
，其中n＝a＋b＋c＋d)
设命题p：(4x－3)2≤1；命题q：x2－(2a＋1)x＋a(a＋1)≤0，若
是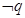
的必要不充分条件，求实数a的取值范围．