（本小题满分12分）
已知m>1，直线
，椭圆C：
，
、
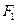分别为椭圆C左、右焦点.
（Ⅰ）当直线过右焦点时，求直线的方程;
（Ⅱ）设直线与椭圆C交于A、B两点，△A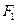、△B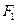的重心分别为G、H.若原点O在以线段GH为直径的圆内，求实数m的取值范围.
（本小题满分10分）
设f(x)为定义在R上的偶函数，当
时，y＝x；当x>2时，y＝f(x)的图像是顶点在P(3,4),且过点A(2,2)的抛物线的一部分
(1)求函数f（x）在
上的解析式；
(2)在下面的直角坐标系中直接画出函数f（x）的图像；
(3)写出函数f(x)值域。
（本小题满分8分）
已知函数y=
-ax-3(
)
(1)若a=2，求函数的最大最小值（2）若函数是单调函数求a取值的范围
（本小题满分8分）
已知全集U=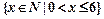
，集合A=｛
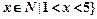，集合B＝
求：（1）
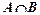
(2) 
已知定义域为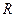
的函数
是奇函数.
（Ⅰ）求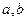
的值；
（Ⅱ）若对任意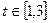
，不等式
恒成立，求实数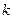
的取值范围.
已知x满足不等式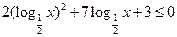
，求
的
最大值与最小值及相应x值．