(本大题8分)已知正方体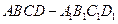 ,求:
,求:
(1)异面直线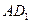 与
与 所成的角;
所成的角;
(2)证明:直线 //平面
//平面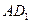 C
C
(3)二面角D— A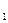 B—C
B—C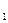 的大小;
的大小;
(本题10分)已知函数 是奇
是奇
函数,当x>0时,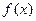 有最小值2,且f (1)
有最小值2,且f (1)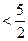 .
.
(Ⅰ)试求函数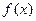 的解析式;
的解析式;
(Ⅱ)函数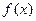 图象上是否存在关于点(1,0)对称的两点?若存在,求出点的坐标;若不存在,说明理由.
图象上是否存在关于点(1,0)对称的两点?若存在,求出点的坐标;若不存在,说明理由.
(本题10分)解关于x的不等式: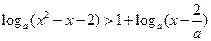 (a>0,a≠1).
(a>0,a≠1).
设数列{an}的前n项和为Sn,a1=1,Sn=nan-2n(n-1).
(1)求数列{an}的通项公式an;
(2)设数列{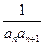 }的前n项和为Tn,
}的前n项和为Tn, 求证:
求证: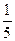 ≤Tn<
≤Tn<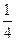 .
.
如图所示,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值.
在 ABC中,内角A,B,C的对边
ABC中,内角A,B,C的对边 分别为a,b,c.已知
分别为a,b,c.已知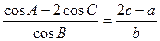 .
.
(I)求 的值;
的值;
(II)若cosB= ,b=2,求△ABC的面积S。
,b=2,求△ABC的面积S。