宇航员在地球表面以一定初速度竖直上 抛一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处。(取地球表面重力加速度g=10 m/s2,空气阻力不计)
抛一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处。(取地球表面重力加速度g=10 m/s2,空气阻力不计)
⑴求该星球表面附近的重力加速度g/;
⑵已知该星球的半径与地球半径之比为R星:R地=1:4,求该星球与地球质量之比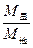 和两星球第一宇宙速度之比
和两星球第一宇宙速度之比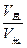
如图所示,半径R=0.5m的光滑圆弧面CDM分别与光滑斜面体ABC和斜面MN相切于C、M点,O为圆弧圆心,D为圆弧最低点.斜面体ABC固定在地面上,顶端B安装一定滑轮,一轻质软细绳跨过定滑轮(不计滑轮摩擦)分别连接小物块P、Q (两边细绳分别与对应斜面平行),并保持P、Q两物块静止.若PC间距为L1=0.25m,斜面MN足够长,物块P质量m1= 3kg,与MN间的动摩擦因数 ,求:(sin37°=0.6,cos37°=0.8)
,求:(sin37°=0.6,cos37°=0.8)
(1)烧断细绳后,物块P第一次到达D点时对轨道的压力大小;
(2)物块P第一次过M点后0.3s到达K点,则 MK间距多大;
(3)物块P在MN斜面上滑行的总路程.
一位同学在用气垫导轨探究动量守恒定律时,测得滑块A以0.095m/s的速度水平向右撞上同向滑行的滑块B,碰撞前B的速度大小为0.045m/s,碰撞后A、B分别以0.045m/s、0.07m/s的速度继续向前运动。求:A、B两滑块的质量之比。
如图所示是一列简谐波在t=0时的波形和传播距离。波沿x轴的正向传播,已知从t=0到t="2.2" s时间内,质点P三次出现在波峰位置。且在t="2.2" s时P质点刚好在波峰位置。求:①该简谐波的周期。②从t=0开始经过多长时间另一质点Q第一次到达波峰。
如图所示,一根长为L的绝缘轻绳的一端固定在O点,另一端连接着一个带正电的小球,小球可视为质点,其质量为m,电荷量为q。在O点正上方和正下方距O点L处,各固定一个绝缘弹性挡板A和B,两个挡板尺寸很小,均竖直放置。此装置处在一个竖直匀强电场中,电场强度的大小为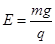 ,方向最初竖直向上。现将小球拉到O点右侧同一高度且距O点L处,给它一个竖直向上的初速度
,方向最初竖直向上。现将小球拉到O点右侧同一高度且距O点L处,给它一个竖直向上的初速度 。此后小球在A、B之间的右侧区域竖直面内做圆周运动,并不时与A、B挡板碰撞,在小球与A、B挡板碰撞时,通过两挡板上安装的传感器和控制电路,控制电场方向在碰后瞬间反向,不计碰撞中的能量损失,重力加速度为g,求:
。此后小球在A、B之间的右侧区域竖直面内做圆周运动,并不时与A、B挡板碰撞,在小球与A、B挡板碰撞时,通过两挡板上安装的传感器和控制电路,控制电场方向在碰后瞬间反向,不计碰撞中的能量损失,重力加速度为g,求:
(1)小球与A挡板第一次碰前瞬间,绳中拉力F1为多少?
(2)小球与B挡板第一次碰前瞬间,绳中的拉力F2为多少?
(3)若轻绳可以承受的最大拉力为50mg,则在绳断之前,小球与B挡板碰撞了多少次?
如图所示电路中,电流表和电压表均为理想电表, ,开始时,电流表读数为0.75A,电压表读数为2V。后来由于某一电阻断路,使电流表读数变为0.8A,电压表读数变为3.2V。
,开始时,电流表读数为0.75A,电压表读数为2V。后来由于某一电阻断路,使电流表读数变为0.8A,电压表读数变为3.2V。
(1)判断是哪一只电阻断路(不用说明理由);
(2)求电源电动势和内电阻。