已知椭圆中心在原点,焦点在
 x轴上,长轴长等于12,离心率为
x轴上,长轴长等于12,离心率为 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ )过椭圆左顶点作直线l垂直于x轴
)过椭圆左顶点作直线l垂直于x轴 ,若动点M到椭圆右焦点的距离比它到直线l的距离小4,求点M的轨迹方程.
,若动点M到椭圆右焦点的距离比它到直线l的距离小4,求点M的轨迹方程.
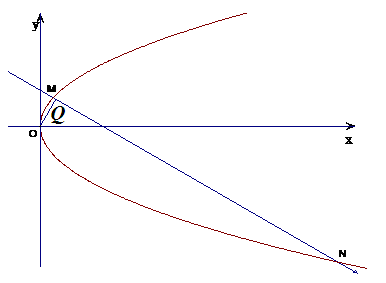
如图,已知直线与抛物线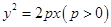 交于
交于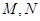 两点,点
两点,点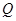 的坐标为
的坐标为 ,
,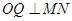 交
交 于点
于点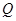 ,
, 抛物线的焦点为
抛物线的焦点为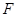 .
.
(1)求 的值;
的值;
(2)记条件(1)所求抛物线为曲线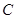 ,过点
,过点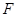 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线 ,设
,设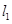 与曲线
与曲线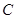 相交于点
相交于点 ,
,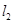 与曲线
与曲线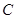 相交于点
相交于点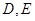 ,求·的最小值.
,求·的最小值.
已知函数 其中
其中 为参数.
为参数.
(1)记函数 ,讨论函数
,讨论函数 的单调性;
的单调性;
(2)若曲线 与
与 轴正半轴有交点且交点为
轴正半轴有交点且交点为 ,曲线在点
,曲线在点 处的切线方程为
处的切线方程为 ,求证:对于任意的正实数
,求证:对于任意的正实数 ,都有
,都有 .
.
已知正项等比数列
 ,首项
,首项 ,前
,前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
已知四棱锥 中
中 平面
平面 ,点
,点 在棱
在棱 上,且
上,且 ,底面为直角梯形,
,底面为直角梯形,

 分别是
分别是 的中点.
的中点.
(1)求证: // 平面
// 平面 ;
;
(2)求截面 与底面
与底面 所成二面角的大小.
所成二面角的大小.
设锐角△ 的三内角
的三内角 的对边分别为
的对边分别为  .
.
(1)设向量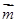
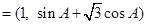 ,
,
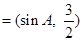 ,若
,若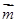 与
与 共线,求角
共线,求角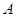 的大小.
的大小.
(2)若 ,
,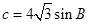 ,且△
,且△ 的面积小于
的面积小于 ,求角
,求角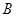 的取值范围.
的取值范围.