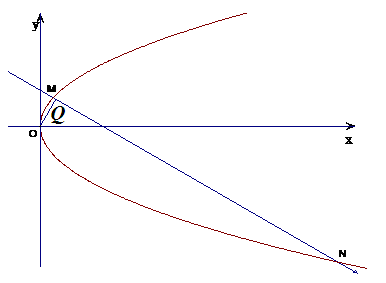
如图,已知直线与抛物线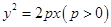 交于
交于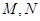 两点,点
两点,点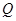 的坐标为
的坐标为 ,
,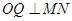 交
交 于点
于点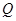 ,
, 抛物线的焦点为
抛物线的焦点为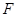 .
.
(1)求 的值;
的值;
(2)记条件(1)所求抛物线为曲线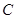 ,过点
,过点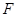 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线 ,设
,设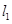 与曲线
与曲线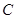 相交于点
相交于点 ,
,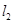 与曲线
与曲线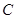 相交于点
相交于点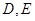 ,求·的最小值.
,求·的最小值.
.如图5,四棱锥 中,底面
中,底面 为矩形,
为矩形,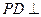 底面
底面 ,
, ,
, 分别为
分别为 的中点
的中点
(1)求证: 面
面 ;
;
(2)若 ,求
,求 与面
与面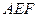 所成角的余弦值
所成角的余弦值
.将10个白小球中的3个染成红色,3个染成兰色,试解决下列问题:
(1)求取出3个小球中红球个数 的分布列和数学期望;
的分布列和数学期望;
(2)求取出3个小球中红球个数多于白球个数的概率
若向量 ,且
,且
(1)求 ;
;
(2)求函数 的值域
的值域
已知直线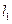
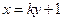 所经过的定点
所经过的定点 恰好是椭圆
恰好是椭圆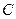 的一个焦点,且椭圆
的一个焦点,且椭圆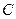 上的点到点
上的点到点 的最大距离为3.
的最大距离为3.
(Ⅰ)求椭圆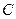 的标准方程;
的标准方程;
(Ⅱ)已知圆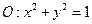 ,直线
,直线 .试证明:当点
.试证明:当点 在椭圆
在椭圆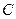 上运动时,直线
上运动时,直线 与圆
与圆 恒相交,并求直线
恒相交,并求直线 被圆
被圆 所截得弦长
所截得弦长 的取值范围.
的取值范围.
(Ⅲ)设直线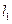 与椭圆交于
与椭圆交于 两点,若直线
两点,若直线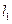 交
交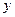 轴于点
轴于点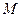 ,且
,且 ,当
,当 变化时,求
变化时,求 的值;
的值;
已知函数 处有两上不同的极值点,设
处有两上不同的极值点,设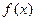 在点
在点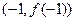 处切线为
处切线为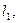 其斜率为
其斜率为 ;在点
;在点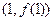 利的切线为
利的切线为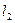 ,其斜率为
,其斜率为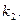
(1)若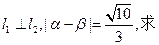
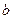 和
和 的值
的值
(2)若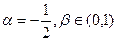 ,求
,求 的取值范围。
的取值范围。