(本小题满分12分)
一次数学模拟考试,共12道选择题,每题5分,共计60分,每道题有四个可供选择的答案,仅一个是正确的。学生小张只能确定其 中10道题的正
中10道题的正 确答案,其余2道题完全靠猜测回答。
确答案,其余2道题完全靠猜测回答。
(I)求小张仅答错 一道选择题的概率;
一道选择题的概率;
(II)小张所在班级共有60人,此次考试选择题得分情况统计表:
| 得分 |
40 |
45 |
50 |
55 |
60 |
| 百分率 |
15% |
10% |
25% |
40% |
10% |
现采用分层 抽样的方法从此班抽取20人的试卷进行选
抽样的方法从此班抽取20人的试卷进行选 择题质量分析。
择题质量分析。
(i)应抽取多少 张选择题得60分的试卷
张选择题得60分的试卷 ?
?
(ii)若小张选择题得60分,求他的试卷被抽到的概率。
已知函数
(Ⅰ)讨论函数 的单调性
的单调性
(Ⅱ)若函数 与函数
与函数 的图像关于原点对称且
的图像关于原点对称且 就函数
就函数 分别求解下面两问:
分别求解下面两问:
①问是否存在过点 的直线与函数
的直线与函数 的图象相切? 若存在,有多少条?若不存在,说明理由.
的图象相切? 若存在,有多少条?若不存在,说明理由.
②求证:对于任意正整数 ,均有
,均有 (
( 为自然对数的底数)
为自然对数的底数)
已知中心在坐标原点,焦点在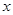 轴上的椭圆过点
轴上的椭圆过点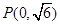 ,且它的离心率
,且它的离心率 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)与圆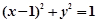 相切的直线
相切的直线 交椭圆于
交椭圆于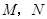 两点,若椭圆上一点
两点,若椭圆上一点 满足
满足 ,求实数
,求实数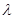 的取值范围.
的取值范围.
如图1,平行四边形 中,
中, ,
, 为
为 中点,将
中点,将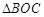 沿
沿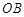 边翻折,折成直二面角
边翻折,折成直二面角 ,
, 为
为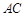 中点,
中点,
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求直线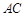 与平面
与平面 所成夹角的正弦值.
所成夹角的正弦值.
已知函数 的部分图象如图所示.
的部分图象如图所示.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)在△ 中,角
中,角 的对边分别是
的对边分别是 ,若
,若 ,求
,求 的取值范围.
的取值范围.
已知数列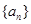 满足
满足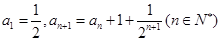
(Ⅰ)求证:数列 成等差数列;
成等差数列;
(Ⅱ)求数列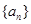 的前
的前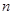 项的和
项的和