某地建一座桥,两端的桥墩已建好,这两墩相距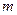 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为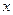 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为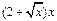 万元。假设桥墩等距离分布,所有桥墩视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩视为点,且不考虑其他因素,记余下工程的费用为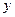 万元。
万元。
(1)试写出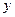 关于
关于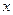 的函数关系式;
的函数关系式;
(2)当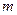 =640米时,需新建多少个桥墩才能使
=640米时,需新建多少个桥墩才能使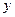 最小?
最小?
(本小题满分14分)
如图,四棱锥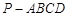 的底面
的底面 为菱形,
为菱形,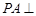 平面
平面 ,
, , E、F分别为
, E、F分别为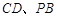 的中点,
的中点, .
.
(Ⅰ)求证:平面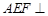 平面
平面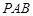 .
.
(Ⅱ)求平面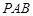 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(本小题满分14分)
已知函数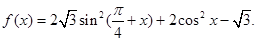
(1)求函数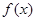 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)已知 内角A,B,C的对边分别为
内角A,B,C的对边分别为 ,若向量
,若向量 共线,求
共线,求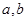 的值。
的值。
(本小题满分12分)
已知函数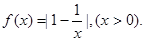
(1)是否存在实数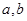
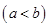 ,使得函数
,使得函数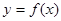 的定义域、值域都是
的定义域、值域都是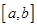 ,若存在,则求出
,若存在,则求出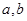 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(2)若存在实数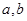
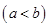 ,使得函数
,使得函数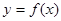 的定义域为
的定义域为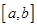 时,值域为
时,值域为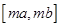 (
(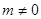 ),求
),求 的取值范围.
的取值范围.
(本小题满分12分)
设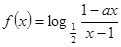 为奇函数,a为常数。
为奇函数,a为常数。
(1)求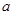 的值;并证明
的值;并证明 在区间
在区间 上为增函数;
上为增函数;
(2)若对于区间 上的每一个
上的每一个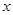 的值,不等式
的值,不等式 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(本小题满分12分)
已知函数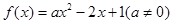 .
.
(1)若函数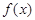 有两个零点,求
有两个零点,求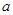 的取值范围;
的取值范围;
(2)若函数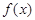 在区间
在区间 与
与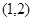 上各有一个零点,求
上各有一个零点,求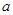 的取值范围.
的取值范围.