(本小题满分12分)
设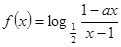 为奇函数,a为常数。
为奇函数,a为常数。
(1)求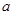 的值;并证明
的值;并证明 在区间
在区间 上为增函数;
上为增函数;
(2)若对于区间 上的每一个
上的每一个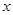 的值,不等式
的值,不等式 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.
(1)当a=-2时,求不等式f(x)<g(x)的解集;
(2)设a>-1时,且当x∈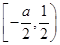 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.
已知a,b为正实数.
(1)求证: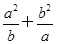 ≥a+b;
≥a+b;
(2)利用(1)的结论求函数y=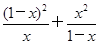 (0<x<1)的最小值.
(0<x<1)的最小值.
如图,AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连结CD.
(1)求证:CD是⊙O的切线;
(2)过点D作DE⊥AB于点E,交AC于点P,求证:P点平分线段DE.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B,E,F,C四点共圆.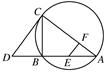
(1)证明:CA是△ABC外接圆的直径;
(2)若DB=BE=EA,求过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值.
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆O于点A,B,C,D,弦AD和BC交于点Q,割线PEF经过点Q交圆O于点E,F,点M在EF上,且∠BAD=∠BMF.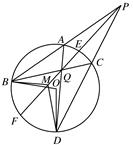
(1)求证:PA·PB=PM·PQ;
(2)求证:∠BMD=∠BOD.