已知正方体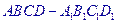 ,
, 是底
是底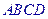 对角线的交点.
对角线的交点.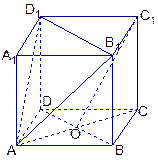
求证:(1)C1O∥面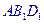 ;
;
(2)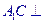 面
面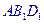 .
.
已知函数 .
.
(1)求 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)设 ,求
,求 的值域.
的值域.
如图,以Ox为始边作角α与β( ) ,它们终边分别单位圆相交于点P、Q,已知点P的坐标为(
) ,它们终边分别单位圆相交于点P、Q,已知点P的坐标为( ,
, ).
).
(1)求 的值;
的值;
(2)若 ·
· ,求
,求 .
.
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 .
.
(1)确定角C的大小:
(2)若c= ,且△ABC的面积为
,且△ABC的面积为
 ,求a+b的值.
,求a+b的值.
已知 ;求
;求 的值.
的值.
用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用一个单位的水可洗掉蔬菜上残留农药的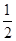 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数 .
.
⑴试规定 的值,并解释其实际意义;
的值,并解释其实际意义;
⑵试根据假定写出函数 应满足的条件和具有的性质;
应满足的条件和具有的性质;
⑶设 ,现有
,现有 单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.