已知 ,函数
,函数 ,
,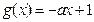 ,
,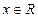 .
.
(I)求函数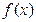 的单调递减区间;
的单调递减区间;
(Ⅱ)若在区间 上至少存在一个实数
上至少存在一个实数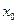 ,使
,使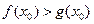 成立,试求正实数
成立,试求正实数 的取值范围.
的取值范围.
(本小题满分12分)
已知斜三棱柱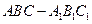 ,
,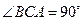 ,
,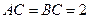 ,
,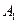 在底面
在底面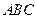 上的射影恰
上的射影恰
为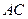 的中点
的中点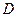 ,
,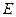 为
为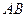 的中点,
的中点,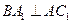 .
.
(I)求证: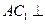 平面
平面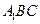 ;
;
(II)求二面角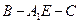 余弦值的大小.
余弦值的大小.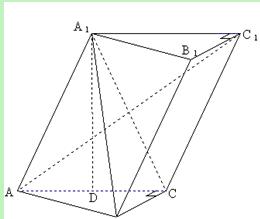
(本小题满分13分)
已知函数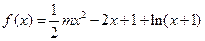
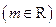
(Ⅰ)当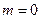 时,求函数
时,求函数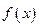 的最大值;
的最大值;
(Ⅱ)当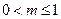 时,曲线
时,曲线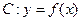 在点
在点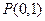 处的切线
处的切线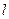 与
与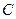 有且只有一个公共
有且只有一个公共
点,求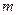 的值.
的值.
(本小题满分13分)
重庆电视台的一个智力游戏节目中,有一道将中国四大名著A、B、C、D与它们的作者
连线的题目,每本名著只能与一名作者连线,每名作者也只能与一本名著连线.每连对
一个得3分,连错得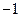 分,一名观众随意连线,将他的得分记作ξ.
分,一名观众随意连线,将他的得分记作ξ.
(Ⅰ)求该观众得分ξ为正数的概率;
(Ⅱ)求ξ的分布列及数学期望.
(本小题满分13分) 已知函数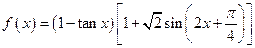 ,求
,求
(Ⅰ)函数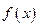 的定义域和值域;
的定义域和值域;
(Ⅱ)写出函数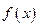 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
1已知函数f(x)=cox2
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)当x0∈(0, )且f(x0)=
)且f(x0)= 时,求f(x0+
时,求f(x0+ )的值.
)的值.