（本小题满分12分）
随机抽取某中学甲乙两个班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图（中间的数字表示身高的百位、十位，旁边的数字分别表示身高的个位数）如图所示。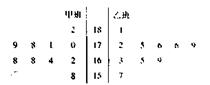
（I）根据茎叶图判断哪个班的平均身高较高；
（II）计算甲班的样本方差；
（III）现从乙班这10名同学中随机抽取两名身高不低于175cm的同学，求身高为176cm的同学被抽中的概率。
(本题满分12分）在
中，
分别是
所对的边长，且满足
.
（1）求角
的大小；
（2）若
，的面积为
，求证：是等边三角形.
(本题满分10分)
已知函数
.
（1）求函数
的最小正周期；
（2）求在
上的最大值和最小值．
椭圆的两焦点坐标分别为F1（
，0），F2（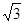
，0），且椭圆过点P（1，
）．
（1）求椭圆方程；
（2）若 A为椭圆的左顶点，作AM⊥AN与椭圆交于两点M、N，试问：直线MN是否恒过x轴上的一个定点？若是，求出该点坐标；若不是，请说明理由．
若椭圆C1：
的离心率等于
，抛物线C2：x2＝2py（p>0）的焦点是椭圆C1的一个顶点．
（1）求抛物线C2的方程；
（2）若过M（－1,0）的直线l与抛物线C2交于E、F两点，又过E、F作抛物线C2的切线l1、l2，当l1⊥l2时，求直线l的方程．
已知二次函数y＝f（x）的图象经过坐标原点，其导函数f ′（x）＝2x＋2，数列{an}的前n项和为Sn，点（n，Sn）（n∈N*）均在函数y＝f（x）的图象上．
（1）求数列{an}的通项公式；
（2）设bn＝2n·an，Tn是数列{bn}的前n项和，求Tn．