(本题满分14分)
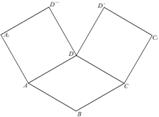
如图1,在平面内,ABCD是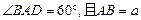 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).

(Ⅰ) 设二面角E – AC – D1的大小为q,若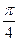 £q£
£q£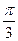 ,求线段BE长的取值范围;
,求线段BE长的取值范围;
(Ⅱ)在线段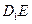 上存在点
上存在点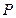 ,使平面
,使平面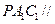 平面
平面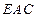 ,求
,求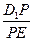 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有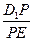 < 1.
< 1.