(本题12分)
研究问题:“已知关于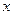 的不等式
的不等式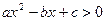 的解集为
的解集为 ,解关于
,解关于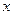 的不等式
的不等式 ”,有如下解法:
”,有如下解法:
解:由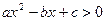
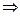
 ,令
,令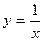 ,则
,则 ,
,
所以不等式 的解集为
的解集为 .
.
参考上述解法,已知关于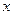 的不等式
的不等式 的解集为
的解集为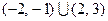 ,求关于
,求关于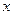 的不等式
的不等式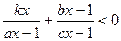 的解集.
的解集.
(本小题满分12分)
2010年11月在广州召开亚运会,某小商品公司开发一种亚运会纪念品,每件产品的成本是15元,销售价是20元,月平均销售a件,通过改进工艺,产品的成本不变,质量和技术含金提高,市场分析的结果表明:如果产品的销售价提高的百分率为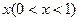 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为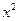 ,记改进工艺后,该公司销售纪念品的月平均利润是y(元)。
,记改进工艺后,该公司销售纪念品的月平均利润是y(元)。
(1)写出y与x的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使该公司销售该纪念品的月平均利润最大。
(本小题满分12分)
2010年夏舟曲发生特大泥石流,为灾后重建,对某项工程进行竞标,现共有6家企业参与竞标,其中A企业来自辽宁省,B、C两家企业来自福建省,D、E、F三家企业来自河南省,此项工程需要两家企业联合施工,假设每家企业中标的概率相同。
(Ⅰ)列举所有企业的中标情况;
(Ⅱ)在中标的企业中,至少有一家来自福建省的概率是多少?
(本题满分14分) 已知数列{an}的前n项和为Sn ,点(n,)在直线y = x +上.数列{bn}满足
bn+2-2bn+1+bn=0(n∈N*),b3=11,且其前9项和为153.
(1)求数列{an},{bn}的通项公式;
(2)设cn=,数列{cn}的前n项和为Tn,求使不等式Tn>对一切n∈N*都成立的最大正整数k的值.
(本题满分14分) 已知函数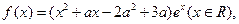 其中
其中
(1)当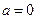 时,求曲线
时,求曲线 处的切线的斜率;
处的切线的斜率;
(2)当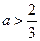 时,求函数
时,求函数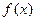 的单调区间与极值。
的单调区间与极值。
(本题满分13分)如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=.
(1)求证:PA⊥B1D1;
(2)求平面PAD与平面BDD1B1所成锐二面角的余弦值.