(本小题12分)
若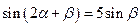 ,证明
,证明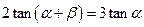
(本小题满分12分)
已知点 和直线
和直线 ,作
,作 垂足为Q,且
垂足为Q,且
(Ⅰ)求点P的轨迹方程;
(Ⅱ)过点C的直线m与点P的轨迹交于两点
 点
点 ,若
,若 的面积为
的面积为 ,求直线
,求直线 的方
的方 程.
程.
(本小题满分12分)
已知定义在R上的函数 的图像关于原点对称,且x=1
的图像关于原点对称,且x=1 时,f(x)取极小值
时,f(x)取极小值 .
.
(Ⅰ)求f(x)的解析式;
(Ⅱ)当x∈[-1,1]时,图像上是否存在两点,使得在此两点处的切线互相垂直?证明你的结 论.
论.
(本小题满分12分)
设数列 为等差数列,且
为等差数列,且 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,
,
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)
如图所示,在正三棱柱 中,底面边长为
中,底面边长为 ,侧棱长为
,侧棱长为 ,
, 是棱
是棱 的中点.
的中点.
|
(Ⅰ)求证: 平面
平面 ;
;
 的大小;
的大小;
 到平面
到平面 的距离.
的距离.
(本小题满分12分)
将一个各个面上均涂有颜色的正方体锯成27个同样大小的小正方体
(Ⅰ)从这些小正方体中任取1个,求其中至少有两面涂有颜色的概率;
(Ⅱ)从中任取2个小正方体,求2个小正方体涂上颜色的面数之和为4的概率。