(本小题满分12分)
设集合A={1,2,3,4,5},集合B={1,2, 3},在A中任取一个数为x,在B中任取一个数为y,组成点(x,y).
(1)写出基本事件空间;
(2)求事件 “x
“x y为偶数”的概率;
y为偶数”的概率;
(3)求事件“xy为奇数”的概率.
已知三点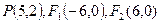
(1).求以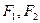 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(2)设点P, 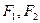 关于直线
关于直线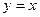 的对称点分别为
的对称点分别为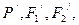 ,求以
,求以 为焦点且过点
为焦点且过点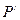 的双曲线的标准方程。
的双曲线的标准方程。
已知 是圆
是圆 上满足条件
上满足条件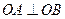 的两个点,其中O是坐标原点,分别过A、B作
的两个点,其中O是坐标原点,分别过A、B作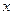 轴的垂线段,交椭圆
轴的垂线段,交椭圆 于
于 点,动点P满足
点,动点P满足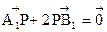 .(1)求动点P的轨迹方程;(2)设
.(1)求动点P的轨迹方程;(2)设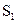 和
和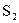 分别表示
分别表示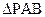 和
和 的面积,当点P在
的面积,当点P在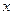 轴的上方,点A在
轴的上方,点A在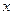 轴的下方时,求
轴的下方时,求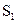 +
+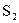 的最大值。
的最大值。
已知函数 .(1)若
.(1)若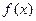 在R上为增函数,求实数
在R上为增函数,求实数 的取值范围;(2)若当
的取值范围;(2)若当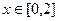 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
已知抛物线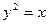 上一点M(1,1),动弦ME、MF分别交
上一点M(1,1),动弦ME、MF分别交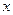 轴与A、B两点,且MA=MB。证明:直线EF的斜率为定值。
轴与A、B两点,且MA=MB。证明:直线EF的斜率为定值。
已知正三棱柱 的侧棱长和底面边长均为2, N为侧棱
的侧棱长和底面边长均为2, N为侧棱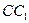 上的点,若平面
上的点,若平面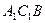 与平面
与平面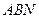 所成二面角(锐角)的余弦值为
所成二面角(锐角)的余弦值为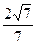 ,试确定点N的位置。
,试确定点N的位置。