设椭圆M: (a>b>0)的离心率与双曲线
(a>b>0)的离心率与双曲线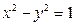 的离心率互为倒数,且内切于圆
的离心率互为倒数,且内切于圆 .
.
(1)求椭圆M的方程;
(2)若直线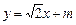 交椭圆于A、B两点,椭圆上一点
交椭圆于A、B两点,椭圆上一点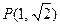 ,
,
求△PAB面积的最大值.
设函数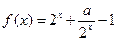 (a为实数)
(a为实数)
(1)当a=0时,若函数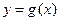 的图象与
的图象与 的图象关于直线x=1对称,求函数
的图象关于直线x=1对称,求函数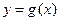 的解析式;
的解析式;
(2)当a<0时,求关于x的方程 =0在实数集R上的解.
=0在实数集R上的解.
设函数f(x)对任意x,y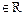 ,都有
,都有 ,且
,且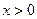 时,f(x)<0,f(1)=-2.
时,f(x)<0,f(1)=-2.
⑴求证:f(x)是奇函数;
⑵试问在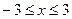 时,f(x)是否有最值?如果有求出最值;如果没有,说出理由.
时,f(x)是否有最值?如果有求出最值;如果没有,说出理由.
若四位数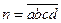 的各位数码
的各位数码 中,任三个数码皆可构成一个三角形的三条边长,则称
中,任三个数码皆可构成一个三角形的三条边长,则称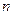 为四位三角形数,试求所有四位三角形数的个数.
为四位三角形数,试求所有四位三角形数的个数.
数列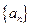 满足:
满足: ;令
;令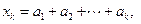
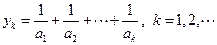 ;求
;求 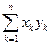
已知椭圆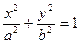 过定点A(1,0),且焦点在x轴上,椭圆与曲线|y|=x的交点为B、C。现有以A为焦点,过点B、C且开口向左的抛物线,抛物线的顶点坐标为M(m,0)。当椭圆的离心率e满足
过定点A(1,0),且焦点在x轴上,椭圆与曲线|y|=x的交点为B、C。现有以A为焦点,过点B、C且开口向左的抛物线,抛物线的顶点坐标为M(m,0)。当椭圆的离心率e满足 时,求实数m的取值范围。
时,求实数m的取值范围。