如图,已知三棱柱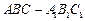 的侧棱与底面垂直,
的侧棱与底面垂直,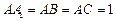 ,
,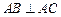 ,M是
,M是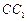 的中点,
的中点,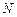 是
是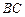 的中点,点
的中点,点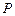 在
在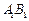 上,且满足
上,且满足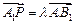 .
.
(1)证明: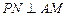 .
.
(2)当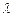 取何值时,直线
取何值时,直线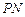 与平面
与平面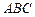 所成的角
所成的角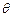 最大?并求该角最大值的正切值.
最大?并求该角最大值的正切值.
(3)若平面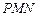 与平面
与平面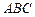 所成的二面角为
所成的二面角为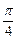 ,试确定P点的位置.
,试确定P点的位置.
已知函数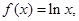 若存在函数
若存在函数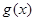 使得
使得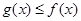 恒成立,则称
恒成立,则称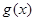 是
是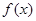 的一个“下界函数”.
的一个“下界函数”.
(I) 如果函数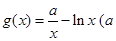 为实数
为实数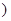 为
为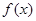 的一个“下界函数”,求
的一个“下界函数”,求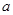 的取值范围;
的取值范围;
(Ⅱ)设函数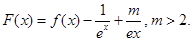 试问函数
试问函数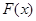 是否存在零点,若存在,求出零点个数;若不存在,请说明理由.
是否存在零点,若存在,求出零点个数;若不存在,请说明理由.
已知椭圆C: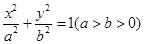 的离心率为
的离心率为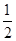 ,右焦点到直线
,右焦点到直线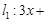
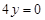 的距离为
的距离为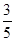 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线 与椭圆C交于A、B两点,且线段AB中点恰好在直线
与椭圆C交于A、B两点,且线段AB中点恰好在直线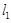 上,求△OAB的面积S的最大值.(其中O为坐标原点).
上,求△OAB的面积S的最大值.(其中O为坐标原点).
已知数列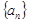 满足
满足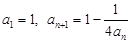 ,其中
,其中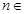 N*.
N*.
(Ⅰ)设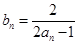 ,求证:数列
,求证:数列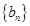 是等差数列,并求出
是等差数列,并求出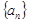 的通项公式
的通项公式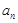 ;
;
(Ⅱ)设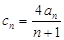 ,数列
,数列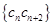 的前
的前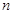 项和为
项和为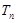 ,是否存在正整数
,是否存在正整数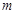 ,使得
,使得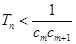 对于
对于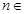 N*恒成立,若存在,求出
N*恒成立,若存在,求出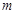 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
已知甲箱中只放有x个红球与y个白球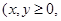 且
且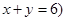 ,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
(Ⅰ)记取出的3个球的颜色全不相同的概率为P,求当P取得最大值时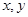 的值;
的值;
(Ⅱ)当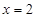 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数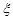 的期望
的期望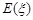 .
.
设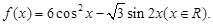 .
.
(Ⅰ)求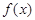 的最大值及最小正周期;
的最大值及最小正周期;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,锐角A满足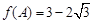 ,
,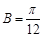 ,求
,求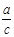 的值.
的值.