(本小题满分12分)
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
 视觉 视觉 |
视觉记忆能力 |
||||
| 偏低 |
中等 |
偏高 |
超常 |
||
| 听觉 记忆 能力 |
偏低 |
0 |
7 |
5 |
1 |
| 中等 |
1 |
8 |
3 |
 |
|
| 偏高 |
2 |
 |
0 |
1 |
|
| 超常 |
0 |
2 |
1 |
1 |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为 .
.
(1)试确定 、
、 的值;
的值;
(2)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(3)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为 ,求随机变量
,求随机变量 的数学期望
的数学期望 .
.
设椭圆C: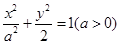 的左、右焦点分别为F1、F2,A是椭圆C上的一点,
的左、右焦点分别为F1、F2,A是椭圆C上的一点,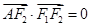 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为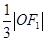 .
.
(1)求椭圆C的方程;
(2)设Q是椭圆C上的一点,过点Q的直线l 交 x 轴于点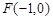 ,交 y 轴于点M,若
,交 y 轴于点M,若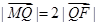 ,求直线l 的斜率.
,求直线l 的斜率.
已知{an}为递增的等比数列,且{a1,a3,a5}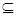 {-10,-6,-2,0,1,3,4,16}.
{-10,-6,-2,0,1,3,4,16}.
(1)求数列{an}的通项公式;
(2)是否存在等差数列{bn},使得a1bn+a2bn-1+a3bn-2+…+anb1=2n+1-n-2对一切n∈N*都成立?若存在,求出bn;若不存在,说明理由.
如图,在四棱锥 中,
中,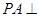 平面
平面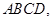 四边形
四边形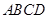 为正方形,
为正方形,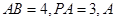 点在
点在 上的射影为
上的射影为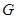 点.
点.
(1)求证: 平面
平面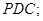
(2)在棱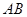 上是否存在一点
上是否存在一点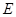 ,使得
,使得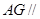 平面
平面 .若存在,求出
.若存在,求出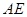 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
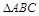 中,角A、B、C对边分别是a、b、c,满足
中,角A、B、C对边分别是a、b、c,满足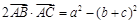 .
.
(1)求角A的大小;
(2)求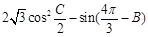 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.
某培训班共有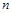 名学生,现将一次某学科考试成绩(单位:分)绘制成频率分布直方图,如图所示.其中落在
名学生,现将一次某学科考试成绩(单位:分)绘制成频率分布直方图,如图所示.其中落在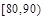 内的频数为36.
内的频数为36.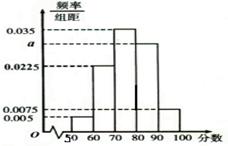
(1)请根据图中所给数据,求出a及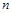 的值;
的值;
(2)从如图5组中按分层抽样的方法选取40名学生的成绩作为一个样本,求在第一组、第五组(从左到右)中分别抽取了几名学生的成绩?
(3)在(2)抽取的样本中的第一与第五组中,随机抽取两名学生的成绩,求所取两名学生的平均分不低于70分的概率.